Hola, quería saber si mi resolución del ejercicio 4 de la sección 5 de la parte a es correcta, además me gustaría saber como se deduce la formula dada
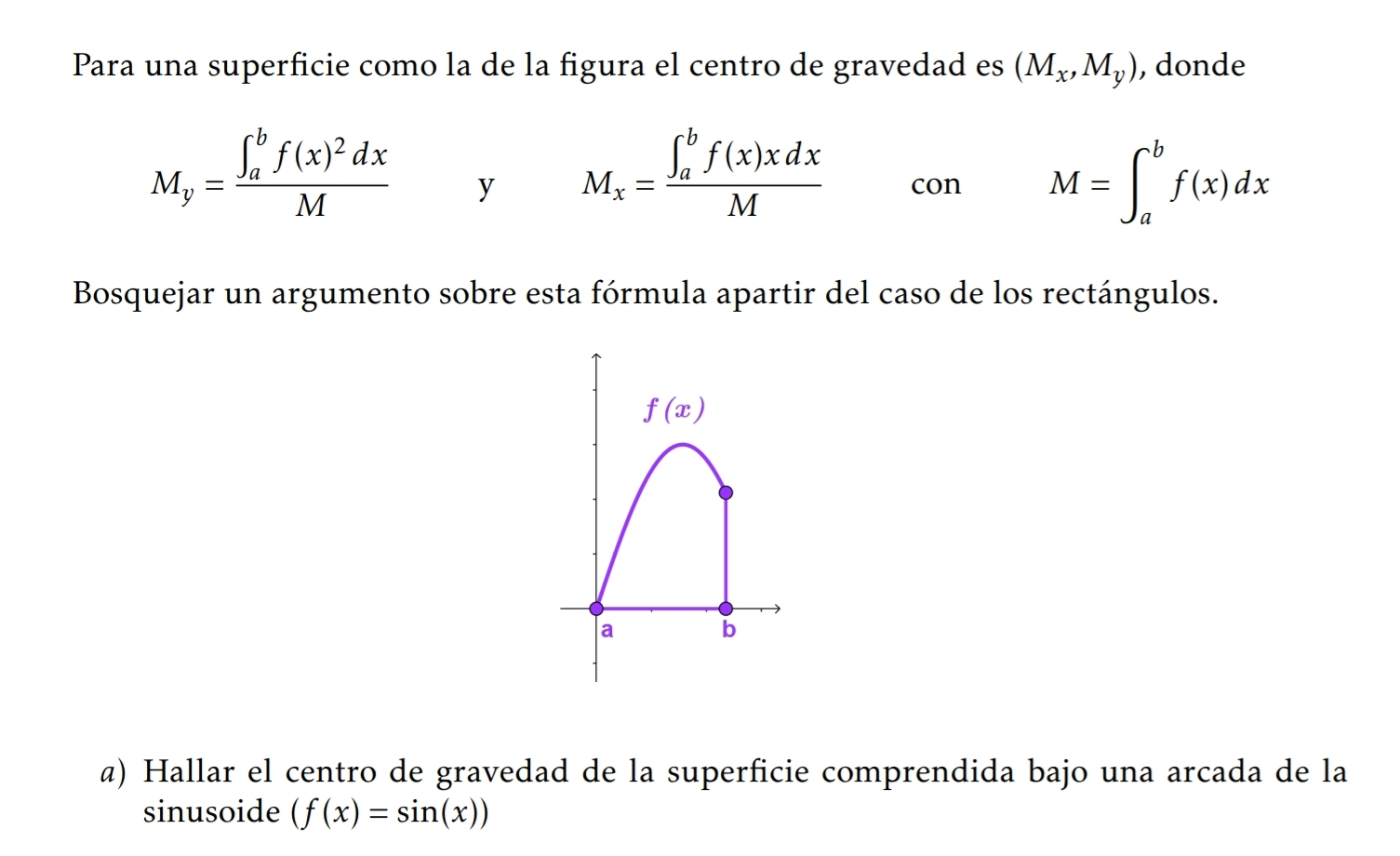
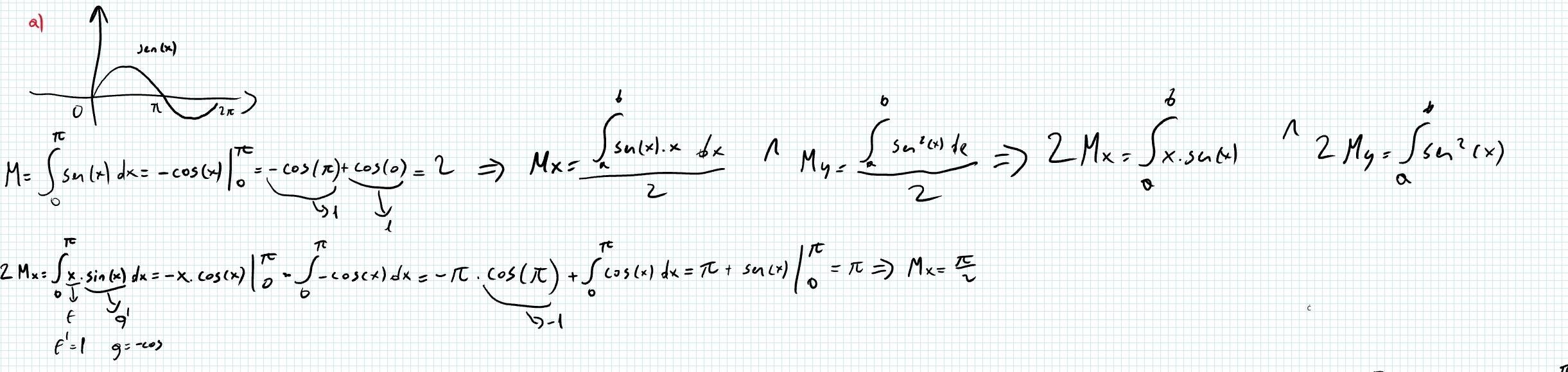
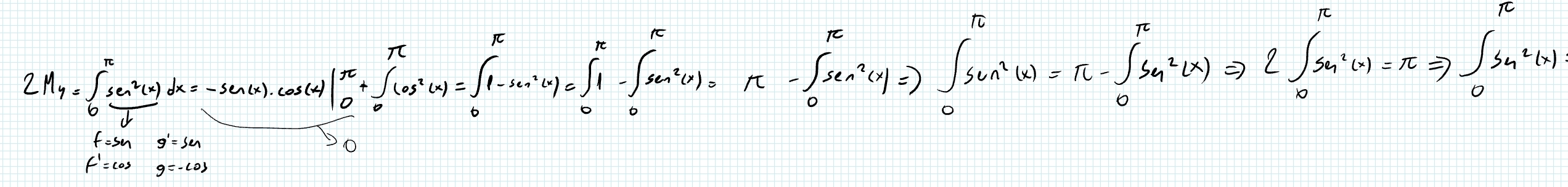
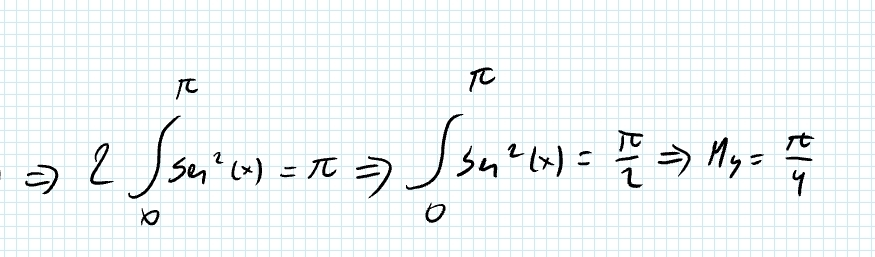
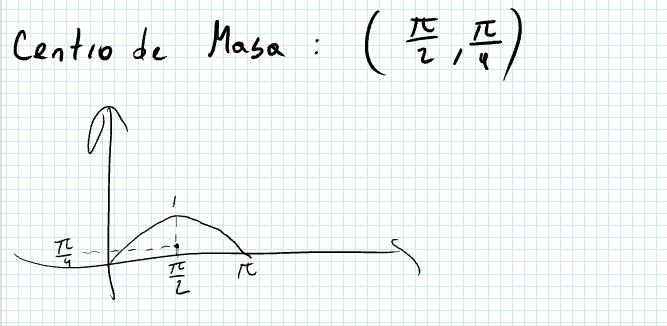
Hola, quería saber si mi resolución del ejercicio 4 de la sección 5 de la parte a es correcta, además me gustaría saber como se deduce la formula dada

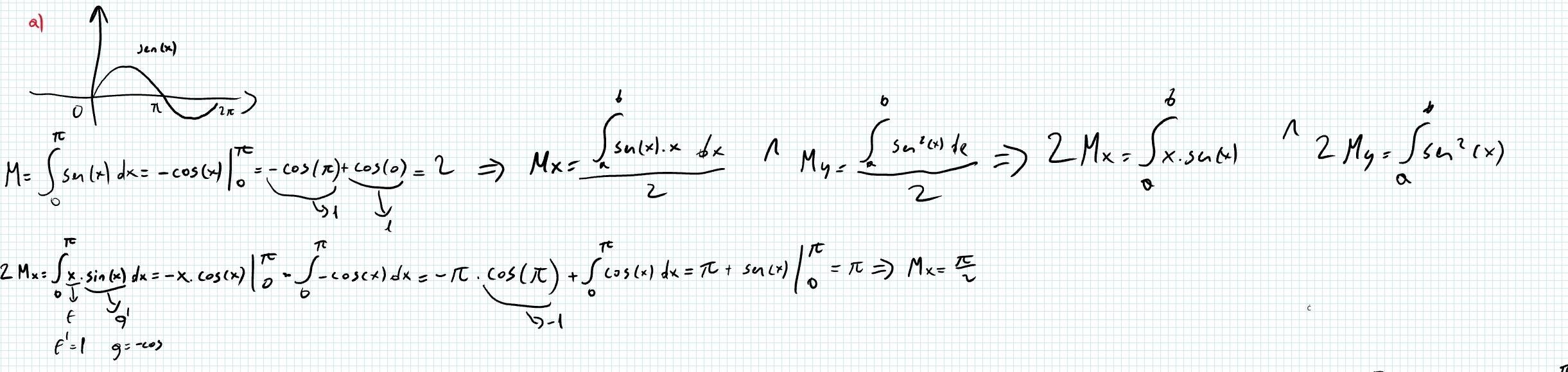
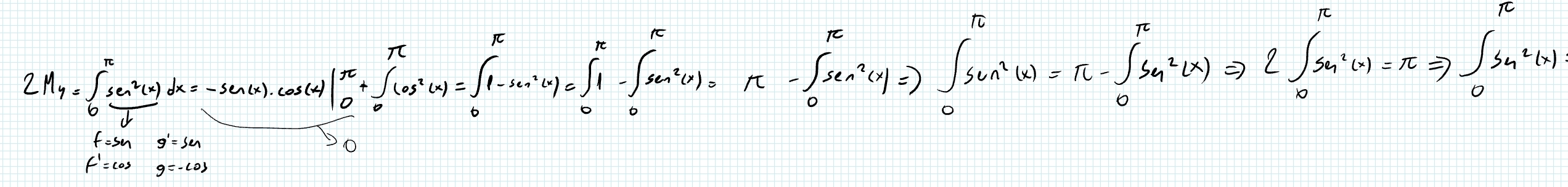
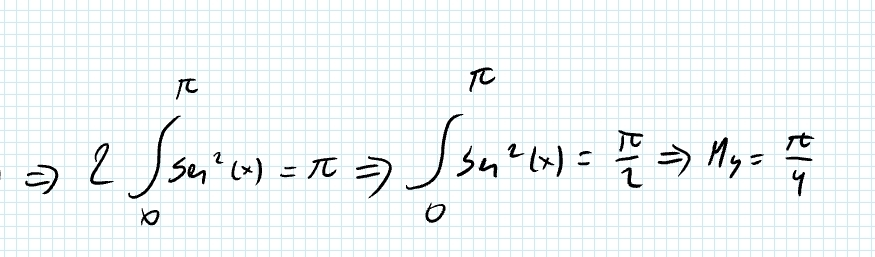

Buenas
Primero, las cuentas están bien
Sobre la intuición, de por que son esas las fórmulas, se pueden intuir de varias maneras. Pero ten en cuenta que no se pedía como parte del ejercicio
Primero, La fórmula de 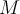 corresponde a la masa, para un objeto de densidad uniforme (igual a 1 pero podría ser cualquier constante). Pues estamos calculando el área y si la densidad del objeto es uniforme, la masa total es área por densidad de masa.
corresponde a la masa, para un objeto de densidad uniforme (igual a 1 pero podría ser cualquier constante). Pues estamos calculando el área y si la densidad del objeto es uniforme, la masa total es área por densidad de masa.
Veamos ejemplos para  . Que ocurre cuando queremos calcular el centro de masa de un sistema finito de partículas en un espacio unidimensional. En ese caso si tenemos partículas
. Que ocurre cuando queremos calcular el centro de masa de un sistema finito de partículas en un espacio unidimensional. En ese caso si tenemos partículas  de masas
de masas  en las posiciones
en las posiciones  , entonces el centro de masa es
, entonces el centro de masa es 
Si interpretamos 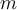 como una función de
como una función de  tenemos la formula, en versión sumatoria, de
tenemos la formula, en versión sumatoria, de  .
.
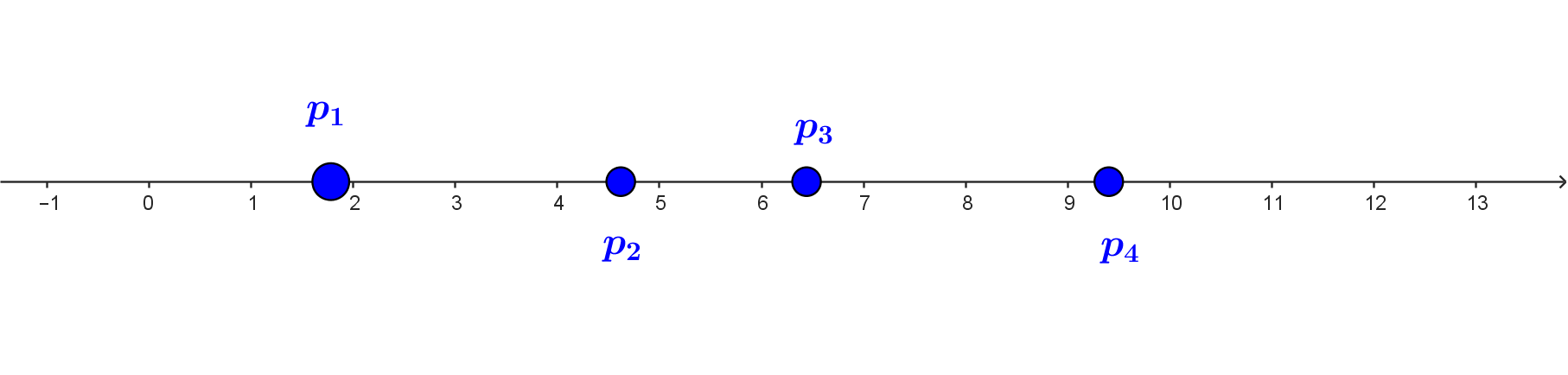
Veamos ahora una idea de como pasar este concepto a continuo.
Esta misma formula discreta vale si tienes finitos cuerpos para los cuales sabes el centro de masa, aunque dichos cuerpos no sean puntuales.
Si tienes cuerpos  con masas
con masas  y centros de masa con coordenadas en el eje x
y centros de masa con coordenadas en el eje x  entonces el centro de masa del sistema, en la coordenada
entonces el centro de masa del sistema, en la coordenada  es
es 

En el ejemplo (dibujo) tomando todos los rectángulos con la misma densidad tenemos 
Como pasamos entonces de estas formulas a la integral. Recordando las sumas superiores o inferiores
Asumiendo que no hay problema con el "pasaje al límite" puedes tomar los rectángulos de una suma inferior equispaseada. Esos rectángulos tienen como altura "el valor de la función en un punto" y como base 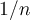 por el tamaño del intervalo.
por el tamaño del intervalo.

Cuando calculas la integral de la función  calculas las áreas de esos rectángulos base
calculas las áreas de esos rectángulos base ![[x_{i},x_{i+1}] [x_{i},x_{i+1}]](https://eva.fing.edu.uy/filter/tex/pix.php/a88ca58e3e75dfeabf27cb3f9feb797c.png) altura "
altura "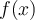 " sin embargo para el centro de masa debes agregar también la coordenada en
" sin embargo para el centro de masa debes agregar también la coordenada en  que seria el punto intermedio del intervalo. Es decir, siendo muy informal la suma quedaría
que seria el punto intermedio del intervalo. Es decir, siendo muy informal la suma quedaría
 "
" " que seria una suma para la función
" que seria una suma para la función 
Para  se puede realizar un estudio análogo.
se puede realizar un estudio análogo.
Si quieres puedes ir al practico de los miércoles y viernes a las 16 y tratamos en mas detalle este ejercicio.
Si quieres que sea mas detallado y formal en la prueba, escribo bien cada argumento y lo subo (repito, ten en cuenta que no se pedía que dedujeran esto)
Saludos