Con respecto al práctico, me di cuenta que este ejercicio se hizo de una manera diferente en las clases y el resultado quedo diferente a como yo lo razoné.
En el práctico quedamos que un triangulo de la matriz es (n² - n) / 2. Pero, ¿no debería ser; (n - 1)² / 2? El triangulo de la matriz no cuenta la diagonal, por lo que en cada lado se le resta 1 y no llega hasta n, se queda en n - 1, y el área es justamente (n - 1)(n - 1) / 2.
Esa parte no la termine de entender, ¡de antemano gracias!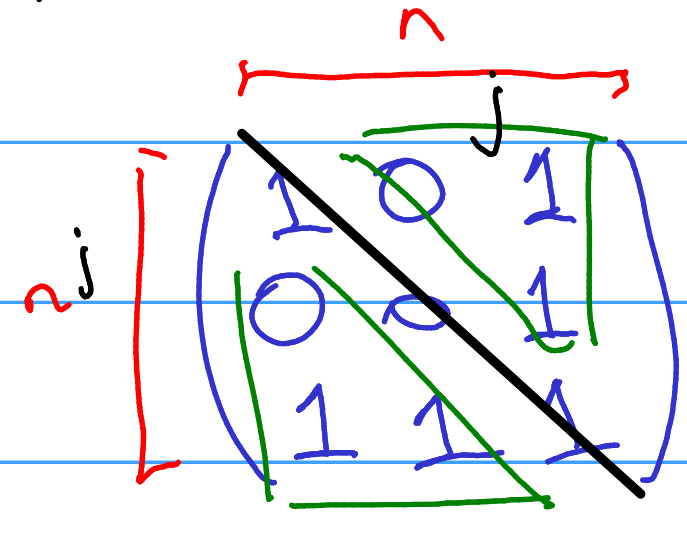
Hola Sebastián.
Estás analizando si la relación es simétrica. Luego, creo entender que los dos triángulos verdes están relacionados de la siguiente manera:
si un término x_{ij}=1, entonces x_{ji}=1, y si x_{ij}=0 entonces x_{ji}=0, con i diferente de j (porque la diagonal no está incluida en los triángulos verdes).
Eso está muy bien. Eso te da libertad de elección (entre 0 y 1) en los n(n-1)/2 términos de un triángulo verde (con lo cual los del otro triángulo verde quedan determinados).
¿Por qué son n(n-1)/2 y no son (n-1)(n-1)/2?
Los términos del triángulo verde son (comenzando a contar desde un vértice, por filas o por columnas):
1 + 2 + 3 + ... + (n-1) = (n-1).n/2
¿Y qué pasa en la diagonal?
Pues en ese caso no importa si ponés 1 o 0 en cada uno de esos términos (porque solo estás analizando si es simétrica o no la relación). Luego, en esos términos (que son n términos) tenés libertad de elección.
En total tenés n(n-1)/2 + n = (n2-n + 2n)/2 = (n2+n)/2 = n(n+1)/2 grados de libertad de elección.
Eso está muy bien. Eso te da libertad de elección (entre 0 y 1) en los n(n-1)/2 términos de un triángulo verde (con lo cual los del otro triángulo verde quedan determinados).
¿Por qué son n(n-1)/2 y no son (n-1)(n-1)/2?
Los términos del triángulo verde son (comenzando a contar desde un vértice, por filas o por columnas):
1 + 2 + 3 + ... + (n-1) = (n-1).n/2
¿Y qué pasa en la diagonal?
Pues en ese caso no importa si ponés 1 o 0 en cada uno de esos términos (porque solo estás analizando si es simétrica o no la relación). Luego, en esos términos (que son n términos) tenés libertad de elección.
En total tenés n(n-1)/2 + n = (n2-n + 2n)/2 = (n2+n)/2 = n(n+1)/2 grados de libertad de elección.
Saludos
Marcelo Lanzilotta