Consultas

Buenas,

En la parte a) del ejercicio se pide calcular el largo medio del archivo codificado. Para hacerlo primero calculé el largo medio de una corrida de ceros en el archivo original, y me dió 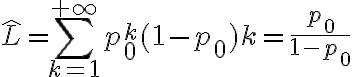$\hat L = \sum_{k=1}^{+\infty} p_0^k(1-p_0)k = \frac{p_0}{1-p_0}$. Cada corrida de ceros en el archivo codificado se codifica con un número (menor que M). Entonces, la cantidad de números en el archivo codificado va a ser la cantidad de corridas de ceros. 

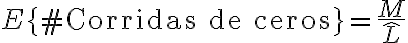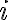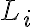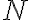Es mi intuición que $E\{\text{#Corridas de ceros}\} = \frac{M}{\hat L}$. 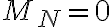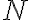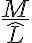No sé si eso está bien ni cómo demostrarlo formalmente, pero la idea es que si la cantidad de bits que restan codificar después de codificar la corrida de ceros $i$ de largo $L_{i}$ es $M_{i} = M_{i-1} - L_{i}$, y el archivo se codifica con $N$ secuencias hasta llegar a $M_{N} = 0$, entonces la esperanza de $N$ es $\frac{M}{\hat L}$ porque la esperanza de 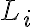$L_{i}$ es $\hat L$.

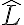Entonces ahi llego a una cantidad de números del archivo de salida, y el largo en bits se calcula multiplicando por la cantidad de bits de la representación binaria de 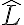$\hat L$.

Mis dudas son: Está bien el razonamiento? Cómo lo demuestro?