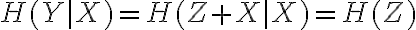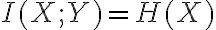Buenas,
En la parte b) de este ejercicio se pide hallar la capacidad del canal con cierta potencia de ruido. No estoy llegando a algo que dependa del ruido.
Usé que la capacidad 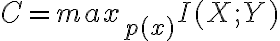 . Luego, que
. Luego, que 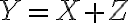 donde
donde 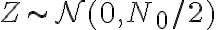 independiente de
independiente de  . Entonces
. Entonces 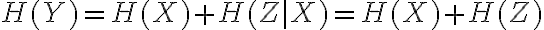 ya que
ya que  no aporta información sobre
no aporta información sobre 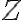 .
.
Entonces 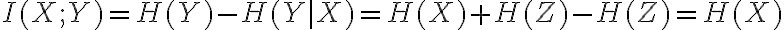 y la información mutua no depende de la potencia de ruido.
y la información mutua no depende de la potencia de ruido.
Entiendo que debería. Dónde me equivoqué?