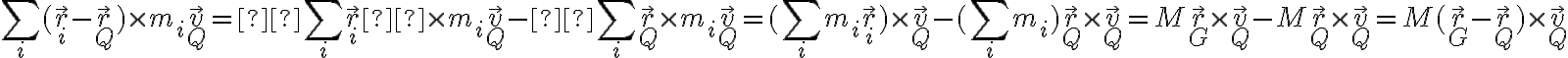Buen día!
Quedé un poco trancado con este ejercicio. Adjunto foto de lo que hice;

No se me ocurre como pasar del término encerrado en rojo a lo que pide el ejercicio. Traté haciendo lo siguiente;

pero me sigue quedando un término que no sé qué es.
Agradezco cualquier ayuda.
Saludos!