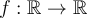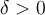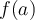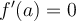Buenas
La definición de extremo relativo es la siguiente
Sea 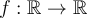 ,
,  tiene un máximo relativo en
tiene un máximo relativo en  si existe un
si existe un 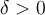 tal que
tal que  para todo
para todo  . En otras palabras si suficientemente cerca de
. En otras palabras si suficientemente cerca de  el mayor valor que toma
el mayor valor que toma  es
es 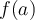 . La definición de mínimo relativo es análoga.
. La definición de mínimo relativo es análoga.
Lo que mencionas relativo a los candidatos es para el estudio de extremos absolutos.
En este ejercicio en particular, para la primera fila, debes entender como son las funciones, ya que no son derivables, y en muchas casos los extremos relativos se darán en puntos donde no son derivables.
En la segunda fila puedes usar la derivada para encontrar los extremos relativos, pero ten en cuenta que son funciones simples que conoces aproximadamente su gráfico, por lo que podrías detectar los extremos relativos incluso sin derivar.
En futuros ejercicios si necesitaras usar la propiedad que si una función derivable tiene un extremo relativo en  entonces
entonces 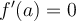 .
.
Si quieres que veamos alguna parte en concreto vuelve a escribir
Saludos