Mi duda es si en este ejercicio tengo que llegar a un valor determinado de a y b, o a una expresión que relacione los valores de a y b pero sin determinar valores numéricos exactos.
Hola Luca.
Debes determinar a y b.
Recuerda que para que f sea derivable en un punto, también tiene que ser continua en ese punto.
Saludos, Florencia.
Debes determinar a y b.
Recuerda que para que f sea derivable en un punto, también tiene que ser continua en ese punto.
Saludos, Florencia.
Hola,
Tengo una consulta sobre eso.
Tengo una consulta sobre eso.
Derivabilidad implica continuidad, pero no al revés. Entonces me queda duda de que tengo que hacer además de plantear continuidad.
Hice esto pero no estoy segura de si está bien, ni de cómo seguir…
Gracias!
Hola Paula.
Por un lado tienes que la función para ser derivable debe ser continua (pero tal como lo decías no será suficiente para que sea derivable).
De todos modos sabes que será necesario que
de dónde deduces que 
, dime si no entiendes por qué.
Ahora bien, necesitamos además que
sea derivable en 
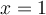para esto calcularemos la derivada usando la definición:
necesitaremos estudiar este límite por izquierda y por derecha ya que la expresión de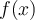 
cambia.
Tenemos entonces que
¿se entiende porqué vale la última igualdad?
Por otro lado tenemos que
Luego, podemos deducir que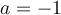
.
Dime si algo no se entendió, saludos, Florencia.
Por un lado tienes que la función para ser derivable debe ser continua (pero tal como lo decías no será suficiente para que sea derivable).
De todos modos sabes que será necesario que
de dónde deduces que , dime si no entiendes por qué.Ahora bien, necesitamos además que
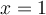sea derivable en para esto calcularemos la derivada usando la definición: necesitaremos estudiar este límite por izquierda y por derecha ya que la expresión de 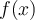cambia.Tenemos entonces que
¿se entiende porqué vale la última igualdad?Por otro lado tenemos que
Luego, podemos deducir que
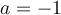.Dime si algo no se entendió, saludos, Florencia.
Hola Flor,
Muchísimas gracias! Ahora si entendí, me había faltado plantear la continuidad antes de la derivabilidad.
Lo único que no entendí fue ¿Por que en el limite por derecha del cociente incremental usaste que a+b=1 y en el de por izquierda no? ¿Podría utilizar esa igualdad en ambas si lo necesitara para calcular el límite?
Gracias!
Muchísimas gracias! Ahora si entendí, me había faltado plantear la continuidad antes de la derivabilidad.
Lo único que no entendí fue ¿Por que en el limite por derecha del cociente incremental usaste que a+b=1 y en el de por izquierda no? ¿Podría utilizar esa igualdad en ambas si lo necesitara para calcular el límite?
Gracias!
Hola Paula, yo utilicé en cada caso la expresión que me convenía para calcular el límite, pero es indistinto.
Saludos, Florencia.
Saludos, Florencia.