Buenas noches, tengo una duda de este ejercicio. No es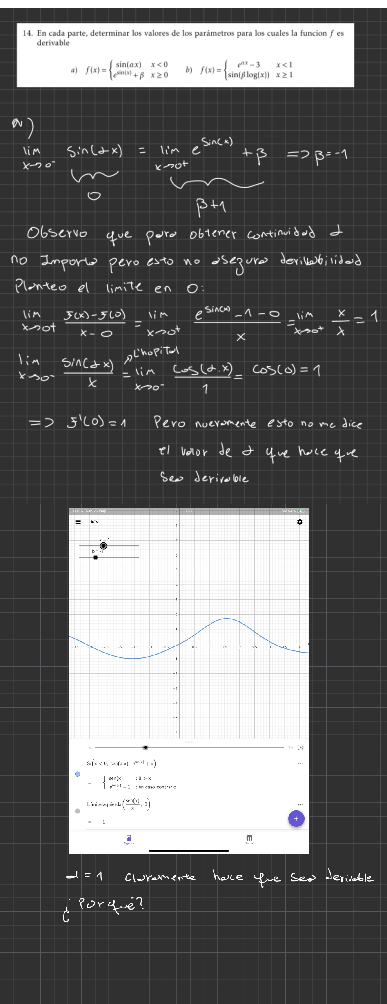 toy seguro de como hallar el valor de alpha para que sea derivable. Lo comento en el archivo adjunto.
toy seguro de como hallar el valor de alpha para que sea derivable. Lo comento en el archivo adjunto.
6.3.14.a "Capitulo 6, Sección 3, EJ 14 parte a"
Número de respuestas: 1
En respuesta a Bruno Sebastián Alvez Da Cruz Martinez
Re: 6.3.14.a "Capitulo 6, Sección 3, EJ 14 parte a"
de Marcos Barrios -
Buenas
En este ejercicio la idea no era usar LHopital, pero una vez que conoces la herramienta no esta mal usarla.
Respecto al primer limite de derivada lateral, cuando planteas
En realidad me gustaría que justificaras esa igualdad. Podrías aplicar LHopital como en el siguiente límite, o bien podrías plantear que para la función  se tiene que
se tiene que  .
.
El problema relativo al 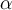 en lo que planteas es que derivaste mal
en lo que planteas es que derivaste mal  , ya que
, ya que 
De esto puedes deducir que 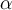 tiene que ser igual a
tiene que ser igual a  .
.
Si tienes mas dudas vuelve a escribir
Saludos
