Buenas
La idea aquí es llevar a las hipótesis de L'Hopital. La funcion esta como una "resta de infinitos" por lo que hay que transformarlo de alguna manera para llevarlo a algo de la forma " " o "
" o "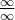 " .
" .
Para esto saquemos de factor común 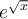 . Mas precisamente
. Mas precisamente
Claramente  por otro lado
por otro lado  de donde
de donde
A partir de alli puedes expresar este producto como " " o "
" o "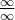 ", pero si tienes dudas de como realizarlo o otras consultas vuelve a escribir
", pero si tienes dudas de como realizarlo o otras consultas vuelve a escribir
Saludos

