Buenas tardes, quería saber como se resuelve el lim de cuando x tiende a infinito de log(x) al cuadrado sobre la raíz de x. Porque apliqué L'Hopital varias veces y me siguen dando indeterminaciones.
Buenas
Primero veamos que estamos en las codiciones de L'Hopital.
Tomando  y
y  tenemos que ambas funciones son derivables en
tenemos que ambas funciones son derivables en 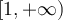 y
y  por lo que efectivamente podemos aplicar la regla de L'Hopital.
por lo que efectivamente podemos aplicar la regla de L'Hopital.
Derivando una vez tenemos que  y
y  .
.
Luego
Recuerda que (una vez verifcado que estas en las hipotesis) la regla de L'Hopital, dice que si existe el limite  entonces es igual a
entonces es igual a  .
.
Pero ahora tenemos este nuevo limite  y para calcularlo podemos aplicar de nuevo L'Hopital pero no para
y para calcularlo podemos aplicar de nuevo L'Hopital pero no para 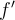 y
y  sino para el numerador y denominador que tenemos en esta nueva expresión.
sino para el numerador y denominador que tenemos en esta nueva expresión.
Intenta continuar desde aqui y cualquier cosa vuelve a escribir
Saludos
