Buenas!, pensándolo como la nota sale bien, pero luego por el otro lado llegue a la integral de : y no se como seguir. El
y no se como seguir. El  lo saque de descomponer los vectores F y P sabiendo además que la Fneta es 0 por la rapidez constante. Desde ya muchas gracias!
lo saque de descomponer los vectores F y P sabiendo además que la Fneta es 0 por la rapidez constante. Desde ya muchas gracias!
Hola, tu expresión para la fuerza 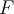 en función del ángulo
en función del ángulo 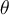 es correcta, pero para calcular el trabajo por medio de la integral hay que tener en cuenta un par de detalles más.
es correcta, pero para calcular el trabajo por medio de la integral hay que tener en cuenta un par de detalles más.
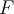 en función del ángulo
en función del ángulo 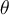 es correcta, pero para calcular el trabajo por medio de la integral hay que tener en cuenta un par de detalles más.
es correcta, pero para calcular el trabajo por medio de la integral hay que tener en cuenta un par de detalles más. Recordemos que la definición de trabajo implica un producto escalar entre la fuerza y el desplazamiento, de modo que lo que hay que tener en cuenta a la hora de realizar la integral no es el módulo de la fuerza como tal, sino la proyección de la fuerza sobre la dirección del desplazamiento, en este caso, la dirección tangencial. Esto significa que en la integral no va simplemente  , sino
, sino  , y se debe integrar en el recorrido de la masa, es decir, sobre el arco de circunferencia que recorre. En general la notación que se usa para esto es la siguiente:
, y se debe integrar en el recorrido de la masa, es decir, sobre el arco de circunferencia que recorre. En general la notación que se usa para esto es la siguiente:
 , sino
, sino  , y se debe integrar en el recorrido de la masa, es decir, sobre el arco de circunferencia que recorre. En general la notación que se usa para esto es la siguiente:
, y se debe integrar en el recorrido de la masa, es decir, sobre el arco de circunferencia que recorre. En general la notación que se usa para esto es la siguiente:Pero nos encontramos con un pequeño obstáculo: tenemos la fuerza escrita en función del ángulo de barrido, pero la integral es en el arco de circunferencia, no en el ángulo. Pero recordemos que conociendo el ángulo de barrido  en radianes, se puede saber el arco de cfa que recorrió la pelota, mediante la relación
en radianes, se puede saber el arco de cfa que recorrió la pelota, mediante la relación  . Podemos usar esta relación sustituyendo en la integral para poder integrar en el ángulo, que era lo que precisábamos !
. Podemos usar esta relación sustituyendo en la integral para poder integrar en el ángulo, que era lo que precisábamos !
 en radianes, se puede saber el arco de cfa que recorrió la pelota, mediante la relación
en radianes, se puede saber el arco de cfa que recorrió la pelota, mediante la relación  . Podemos usar esta relación sustituyendo en la integral para poder integrar en el ángulo, que era lo que precisábamos !
. Podemos usar esta relación sustituyendo en la integral para poder integrar en el ángulo, que era lo que precisábamos !Espero que sirva! Cualquier cosa estoy a las órdenes.
Saludos.
