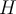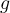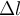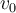Buenas,
estoy teniendo problemas resolviendo la parte (c). Mi versor de referencia es 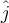 positivo hacia abajo y mi cero está donde la caja comienza su movimiento. De las partes (a) y (b) conozco.
positivo hacia abajo y mi cero está donde la caja comienza su movimiento. De las partes (a) y (b) conozco.
(b)
De cinemática sabemos  , con
, con 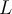 la distancia desde donde comienza el movimiento de la masa hasta el punto de mayor compresion del resorte.
la distancia desde donde comienza el movimiento de la masa hasta el punto de mayor compresion del resorte.
Y por tanto la posición de la masa cuando entra en contacto con el resorte es 
Conzco  , posición, velocidad y aceleracion de la masa respecto al tiempo.
, posición, velocidad y aceleracion de la masa respecto al tiempo.
Despues de hacer cuentas obtuve
Ahora sabiendo 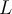 para responder la parte (c) solo me falta conocer la longitud del resorte cuando está comprimido, cosa que no entiendo cómo hacer o siquiera si puedo calcularlo. Además me gustaría saber si lo anterior es correcto.
para responder la parte (c) solo me falta conocer la longitud del resorte cuando está comprimido, cosa que no entiendo cómo hacer o siquiera si puedo calcularlo. Además me gustaría saber si lo anterior es correcto.
Gracias :)