Hola Andrés.
La matriz asociada en base canónica queda  .
.
La segunda columna ya te dice que (0,1,0) es vector propio asociado a  .
.
Sus valores propios son 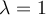 con m.g.=m.a.=1 y
con m.g.=m.a.=1 y  con m.a.=2 y m.g. que presumiblemente dependa de
con m.a.=2 y m.g. que presumiblemente dependa de 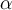 y
y 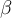 .
.
Por tanto el que T sea o no diagonalizable dependerá de la m.g.( ), o sea de la dim(
), o sea de la dim( ).
).
Cuando operas para hallar  obtienes un sistema del que se deduce x=0, y cualquiera,
obtienes un sistema del que se deduce x=0, y cualquiera,  .
.
Si estudias los dos casos posibles para la ecuación  tendrás los posibles
tendrás los posibles  y podrás determinar la opción correcta.
y podrás determinar la opción correcta.
Saludos
J.