Buenos días, ¿qué tal?
Tengo dificultades para realizar este ejercicio, creo que no comprendo la idea de función de Lipschitz, si pudieran explicarme un poco más sobre de que se trata se los agradezco.
Saludos
Buenos días, ¿qué tal?
Tengo dificultades para realizar este ejercicio, creo que no comprendo la idea de función de Lipschitz, si pudieran explicarme un poco más sobre de que se trata se los agradezco.
Saludos
 es Lipschitz si existe una constante positiva
es Lipschitz si existe una constante positiva 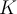 tal que para todo par de puntos
tal que para todo par de puntos 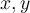 en el dominio de la función se cumple |𝑓(𝑥)−𝑓(𝑦)|≤𝐾|𝑥−𝑦|.|f(x)−f(y)|≤K|x−y|.
en el dominio de la función se cumple |𝑓(𝑥)−𝑓(𝑦)|≤𝐾|𝑥−𝑦|.|f(x)−f(y)|≤K|x−y|.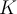 por la distancia entre los puntos. Ejemplos: Las funciones
por la distancia entre los puntos. Ejemplos: Las funciones 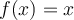 y
y 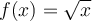 son Lipschitz en su dominio, pero la función
son Lipschitz en su dominio, pero la función 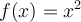 no lo es.
no lo es.