Hola , queria pedir ayuda para poder encarar este ejercicio. Gracias
En respuesta a Melani Scagni Larrañaga
Re: Sección 3.5 ejercicio 4a y b
Hola,
Acordate que el gráfico de la función![f_1:[-1,1]\to\mathbb{R} f_1:[-1,1]\to\mathbb{R}](https://eva.fing.edu.uy/filter/tex/pix.php/d356759579bbdb847516eb6cc766d1fe.png) dada por
dada por  es la mitad del círculo de radio 1, por lo que el área del círculo de radio 1 es
es la mitad del círculo de radio 1, por lo que el área del círculo de radio 1 es  .
.
Ahora, si encontrases una función![f_r:[-r,r]\to\mathbb{R} f_r:[-r,r]\to\mathbb{R}](https://eva.fing.edu.uy/filter/tex/pix.php/6774c4bf3606f457d516f504a34ed2cc.png) cuyo gráfico sea la mitad del círculo de radio r, entonces tendrías que el área del círculo de radio r es
cuyo gráfico sea la mitad del círculo de radio r, entonces tendrías que el área del círculo de radio r es  .
.
Bueno, resulta que a la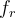 la obtenés a partir de la
la obtenés a partir de la 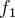 mediante "operaciones lineales". Más en concreto,
mediante "operaciones lineales". Más en concreto,  (podés ir graficando todo lo que digo en geogebra). Lo que está pasando es que contraés el intervalo
(podés ir graficando todo lo que digo en geogebra). Lo que está pasando es que contraés el intervalo ![[-r,r] [-r,r]](https://eva.fing.edu.uy/filter/tex/pix.php/41b4ab49507fdfa895adf70e230ce557.png) hasta el intervalo
hasta el intervalo ![[-1,1] [-1,1]](https://eva.fing.edu.uy/filter/tex/pix.php/d060b17b29e0dae91a1cac23ea62281a.png) cuando dividís por
cuando dividís por 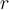 , luego aplicás la función
, luego aplicás la función 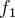 , y luego estirás las imágenes cuando multiplicás por
, y luego estirás las imágenes cuando multiplicás por 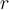 .
.
Bueno, la cuestión es que con la igualdad podés hacer cambio de variable lineal para calcular
podés hacer cambio de variable lineal para calcular  en función de
en función de  .
.
Acordate que el gráfico de la función
![f_1:[-1,1]\to\mathbb{R} f_1:[-1,1]\to\mathbb{R}](https://eva.fing.edu.uy/filter/tex/pix.php/d356759579bbdb847516eb6cc766d1fe.png) dada por
dada por  es la mitad del círculo de radio 1, por lo que el área del círculo de radio 1 es
es la mitad del círculo de radio 1, por lo que el área del círculo de radio 1 es  .
.Ahora, si encontrases una función
![f_r:[-r,r]\to\mathbb{R} f_r:[-r,r]\to\mathbb{R}](https://eva.fing.edu.uy/filter/tex/pix.php/6774c4bf3606f457d516f504a34ed2cc.png) cuyo gráfico sea la mitad del círculo de radio r, entonces tendrías que el área del círculo de radio r es
cuyo gráfico sea la mitad del círculo de radio r, entonces tendrías que el área del círculo de radio r es  .
.Bueno, resulta que a la
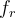 la obtenés a partir de la
la obtenés a partir de la 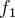 mediante "operaciones lineales". Más en concreto,
mediante "operaciones lineales". Más en concreto,  (podés ir graficando todo lo que digo en geogebra). Lo que está pasando es que contraés el intervalo
(podés ir graficando todo lo que digo en geogebra). Lo que está pasando es que contraés el intervalo ![[-r,r] [-r,r]](https://eva.fing.edu.uy/filter/tex/pix.php/41b4ab49507fdfa895adf70e230ce557.png) hasta el intervalo
hasta el intervalo ![[-1,1] [-1,1]](https://eva.fing.edu.uy/filter/tex/pix.php/d060b17b29e0dae91a1cac23ea62281a.png) cuando dividís por
cuando dividís por 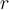 , luego aplicás la función
, luego aplicás la función 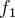 , y luego estirás las imágenes cuando multiplicás por
, y luego estirás las imágenes cuando multiplicás por 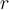 .
.Bueno, la cuestión es que con la igualdad
 podés hacer cambio de variable lineal para calcular
podés hacer cambio de variable lineal para calcular  en función de
en función de  .
.