Consultas del libro de ejercicio - Capítulo 3: Integración

Buenas

Lo mejor es que trates de ver que pasa en ejemplos, por ejemplos la función 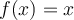$f(x) = x$.

La definicion b dice que para todo epsilon, para toda partición 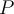$P$ se cumple que $S^{*}(f,P) - S_{*}(f,P) \leq \epsilon$.

Como dice para todo \epsilon, podriamos tomar por ejemplo $\epsilon= 1$ como dice para todo particion podiamos tomar la particion del intervalo [1,5] que solo tiene los puntos 1 y 2.

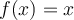En ese caso $S^{*}(f,P) = 5(5-1) = 20$ y $S_{*}(f,P) = 1(5-1) = 4$. Es decir que $f(x) = x$ NO cumple la definicion b. Sin embargo si cumple la definicion a (pues es integrable). Esto nos dice que las definiciones no son equivalentes.

Más alla del ejemplo, para explicarte mejor las relaciones entre las afirmaciones quiza puedes ir a pregutnar y conversar el ejercicio en algun práctico.

Escribo una de las comparaciones.

La afirmación b dice para todo 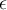$\epsilon$ para toda particion... es decir que sin importar 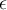$\epsilon$ la condicion se cumple para cualquier particion. Mientras que la definición a dice existe una particion. Queda claro que si se cumple para toda particion entonces existe una para la cual se cumple. Tenemos asi que b implica a.
El ejemplo anterior muestra que a no implica b.

Si tienas mas dudas vuelve a escribir, pero insisto que creo que con este problema en concreto vayas a algun grupo de practico a preguntarlo

Saludos