Buenas,
Quería consultar si está disponible la solución a los ejercicios de este parcial, ya que en la carpeta no la encuentro. Más específicamente, me interesa saber la solución del ejercicio 6.
Buenas,
Quería consultar si está disponible la solución a los ejercicios de este parcial, ya que en la carpeta no la encuentro. Más específicamente, me interesa saber la solución del ejercicio 6.
Buenas
La idea de este ejercicio es revisar las afirmaciones para detectar la correcta.
Voy a irlas enumerando y probando si son falsas o no.
Esta afiramción es falsa. Esta afirmación (observando que 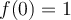 ) corresponde a la definicion de continuidad en 0, y la función
) corresponde a la definicion de continuidad en 0, y la función  no es continua en 0. Para verificar puedes tomar
no es continua en 0. Para verificar puedes tomar  y observar que para todo
y observar que para todo 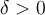 se tiene que
se tiene que 
Esta afirmación es falsa. Intuitivamente la afirmación dice que tan cerca como quieras de 0 tenes puntos  para los cuales
para los cuales 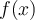 estan tan lejos como quieras de 1. Para verificar que es falsa podemos tomar
estan tan lejos como quieras de 1. Para verificar que es falsa podemos tomar  y
y  , en ese caso para todo
, en ese caso para todo  tal que
tal que  se cumple que
se cumple que  y por tanto
y por tanto 
Esta afirmación es falsa. Basta ver que para todo 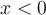 se cumple que
se cumple que 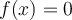 luego no se verifica que
luego no se verifica que 
Esta afirmacion es verdadera. Dados 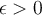 y
y 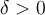 si tomamos
si tomamos  se cumple que
se cumple que  y
y 
Esta afirmación es falsa. La afirmacion es equivalente a que la función  este acotada y no es el caso. Para todo
este acotada y no es el caso. Para todo 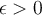 el punto
el punto  verifica que
verifica que 
Esta afirmación es falsa. Esta afirmacion la definicion de continuidad de  en
en  pero con
pero con 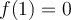 . Puedes argumentar similar a la opción A
. Puedes argumentar similar a la opción A
Ten en cuenta que este ejercicio es MO y que habia un grafico de la función por lo que a la hora de realizar el parcial no era necesario probar formalmente cada opcion.
Cualquier duda vuelve a escribir
Saludos