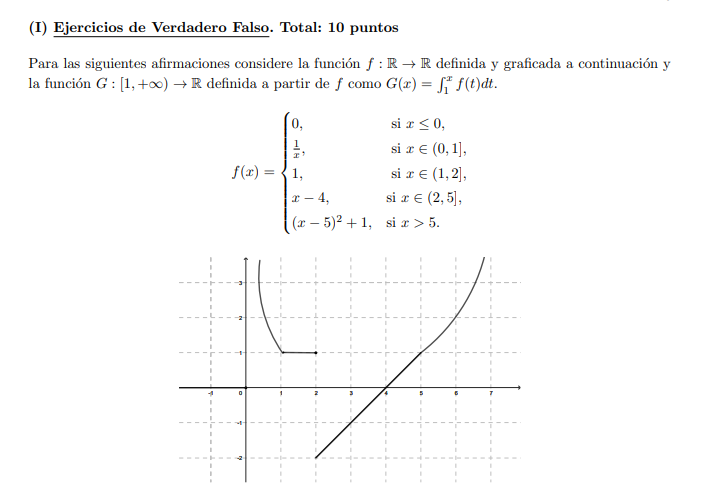
Buenas, estaba practicando con pruebas anteriores y tengo una duda sobre el ejercicio 1 de Verdadero Falso, en la afirmación 5,  me dice que G es continua, y en las respuestas está marcada como verdadera
me dice que G es continua, y en las respuestas está marcada como verdadera . Pero cuando voy integrando y graficando no me queda continua en ese intervalo en 2. No sé bien que estoy haciendo mal me queda x-1 la integral (1,2] y (x^2-1)/2-4x+4 en (2,5]
. Pero cuando voy integrando y graficando no me queda continua en ese intervalo en 2. No sé bien que estoy haciendo mal me queda x-1 la integral (1,2] y (x^2-1)/2-4x+4 en (2,5]
Saludos.

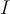


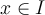
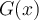
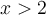
![x \in (2,5] x \in (2,5]](https://eva.fing.edu.uy/filter/tex/pix.php/2020e29005198beee46f010bf6567468.png)

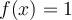
![x \in [2,5] x \in [2,5]](https://eva.fing.edu.uy/filter/tex/pix.php/be6433e20db81173fdde7b2edee38b6d.png)

