Consultas sobre los cuestionarios

Buenas

Primero, basta ver que el problema es equivalente a que una partición 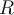$R$ cumpla que $S^{*}(f,R) = S_{*}(f,R)$. Pues podemos tomar $R = P \cup Q$ y en ese caso $S_{*}(f,R) \geq S_{*}(f,P) = S^{*}(f,Q) \geq S^{*}(f,R)$.

Que sea integrable es equivalente a que, dado un margen 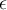$\epsilon$ exista una partición para la cual la suma superior y la suma inferior difiera menos de 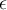$\epsilon$. Proposición 25 de las notas.

Pero esto no quiere decir que necesariamente haya una particion para la cual la diferencia sea 0.

Dada una partición $R=\{p_{0},...,p_{n}\}$, por definicion la suma inferior y la suma superior es

$\displaystyle S_{*}(f,R) = \sum_{i=0}^{n-1} \inf(f,[p_{i},p_{i+1}])(p_{i+1}-p_{i}),\,\,\,\, S^{*}(f,R) = \sum_{i=0}^{n-1} \sup(f,[p_{i},p_{i+1}])(p_{i+1}-p_{i}),$

Esto quiere decir que

$\displaystyle S^{*}(f,R) - S_{*}(f,R) = \sum_{i=0}^{n-1} (\sup(f,[p_{i},p_{i+1}]) - \inf(f,[p_{i},p_{i+1}]))(p_{i+1} - p_{1})$

Como cada término de la suma es mayor o igual a 0, para que $S^{*}(f,R) = S_{*}(f,R)$ se tiene que cumplir que cada sumando es igual a 0.

Es decir $\sup(f,[p_{i},p_{i+1}]) - \inf(f,[p_{i},p_{i+1}]) = 0$- Pero esto ocurre solo si $f$ es constante en el intervalo $[p_{i},p_{i+1}]$

Si tomamos por ejemplo 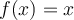$f(x) = x$. Esta función es integrable (por ser monótona) pero la suma superior e inferior no van a ser iguales para ninguna partición (por ser estrictamente creciente) por lo que la afirmación que indica el problema es falsa

Saludos