CDIV-1S: 3.1 - b

Buenas,

Vi en otra consulta la forma de resolver el 3.1 - a) pero no pude usar esa respuesta para formular una para el 3.1 - b), siendo este b) f2(t) = [t].

Analizando el crecimiento de la función f2 puedo ver que F2 crece más rápido cuando f(t) es menor o igual 0,5 y luego crece más lento cuando se reduce la distancia hasta el próximo. ¿Si esto es cierto, como puedo hallar la ecuación explícita de F2 cuando esta cambia de forma en intervalos de 0,5?

Capáz le estoy errando feo pero es lo único que se me ocurre en el momento.

Desde ya muchas gracias.

Re: 3.1 - b

de Tabare Nahuel Roland Silveira - lunes, 8 de abril de 2024, 15:29

Hola,
Por el ejercicio que describís, creo que estás hablando del ejercicio 3.1.6.b.

Primero que nada, recordá como el el gráfico de la función [t], que son un montón de triángulos repetidos.

Para calcular el valor de la función, fijate que dado

$x$ , la integral de [t] desde

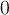
$0$ hasta

$x$ es sumar el área de la cantidad de triángulos enteros que quedan contenidos debajo del gráfico, más un cachito de área más del triángulo que no queda completo. La cantidad de triángulos que quedan completos es parte entera de

$x$ , por lo que el área que eso aporta es parte entera de

$x$ por el área del triángulo.

Ahora, para el área sobrante, la fórmula va a depender de “el número después de la coma” de

$x$ , lo que se puede escribir explícitamente como

$x$ menos parte entera de

$x$ , por lo que te va a quedar una función definida por partes dependiendo de si lo anterior es menor o igual a 0,5 o mayor a 0,5. Tenés que calcular el área según el dibujo que te quede en ese caso, y a eso hay que recordar sumarle el área de todos los triángulos anteriores que describimos en el párrafo anterior.

Fijate si eso te ayuda a pensar el ejercicio. Cualquier cosa, volvé a preguntar.

Saludos!