Hola , me pueden explicar cómo sería ? Porque creo que no puedo aplicar la propiedad de que la suma de integrale de f más g es igual al integral de f.mas integral de g . Por lo tanto como hago ?
Buenas
No entiendo a que ejercicio haces referencia.
Por lo que planteas entiendo que es el ejercicio 3.6-2. En ese caso si puedes usar todas las propiedades vistas para la integral, en particular la aditvidad respecto al intervalo y la linealidad.
Si es otro ejercicio o si tienes dudas de ese vuelve a escribir
Saludos
Me refiero a este ejercicio 10 , son tres integrales , la primera es integral de 1 a 4 de [√x]
En respuesta a Pedro Felipe Freire Dos Santos
Re: ejercicio 3.6.10
Hola,
Si está entre
está entre  y
y 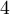 , el valor de
, el valor de 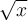 está entre
está entre  y
y 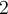 . Luego, el valor de
. Luego, el valor de ![[\sqrt{x}] [\sqrt{x}]](https://eva.fing.edu.uy/filter/tex/pix.php/7c6fc2bb16cf68b384d88b9b1b8924b2.png) depende de si
depende de si  o si
o si 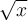 es mayor de 1,5. En caso de que
es mayor de 1,5. En caso de que  , el entero más cercano a
, el entero más cercano a 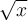 es
es  , por lo que
, por lo que ![[\sqrt{x}] = \sqrt{x}-1 [\sqrt{x}] = \sqrt{x}-1](https://eva.fing.edu.uy/filter/tex/pix.php/d1895b1a19b58388273d8172aaf78295.png) . En caso de que
. En caso de que 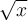 sea mayor a
sea mayor a 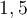 , se tiene que el entero más cercano a
, se tiene que el entero más cercano a 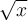 es
es 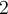 , por lo que
, por lo que ![[\sqrt{x}] = 2-\sqrt{x} [\sqrt{x}] = 2-\sqrt{x}](https://eva.fing.edu.uy/filter/tex/pix.php/f571991132323b0b968ec86d0d148782.png) .
.
Por lo tanto, si encontrás en que punto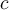 ocurre que
ocurre que  , tenés una fórmula para
, tenés una fórmula para ![[\sqrt{x}] [\sqrt{x}]](https://eva.fing.edu.uy/filter/tex/pix.php/7c6fc2bb16cf68b384d88b9b1b8924b2.png) en el intervalo
en el intervalo ![[1,c] [1,c]](https://eva.fing.edu.uy/filter/tex/pix.php/e7fa0133d10b716aa0dba9dd3d2bccc1.png) y otra para el intervalo
y otra para el intervalo ![[c,4] [c,4]](https://eva.fing.edu.uy/filter/tex/pix.php/c99838766d7fbf2963bea1af3c69d4c8.png) , y en cada caso sabés calcular la integral de la funciones que te quedan (que serían
, y en cada caso sabés calcular la integral de la funciones que te quedan (que serían  en un intervalo y
en un intervalo y  en el otro). Usando la aditividad de la integral, te queda que la integral de
en el otro). Usando la aditividad de la integral, te queda que la integral de ![[\sqrt{x}] [\sqrt{x}]](https://eva.fing.edu.uy/filter/tex/pix.php/7c6fc2bb16cf68b384d88b9b1b8924b2.png) en el intervalo
en el intervalo ![[1,4] [1,4]](https://eva.fing.edu.uy/filter/tex/pix.php/94fe668c80113341416b96929a8f1024.png) es la integral de
es la integral de  de
de  a
a 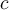 más la integral de
más la integral de  de
de 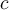 a
a 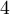 .
.
Saludos!
Si
 está entre
está entre  y
y 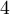 , el valor de
, el valor de 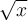 está entre
está entre  y
y 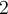 . Luego, el valor de
. Luego, el valor de ![[\sqrt{x}] [\sqrt{x}]](https://eva.fing.edu.uy/filter/tex/pix.php/7c6fc2bb16cf68b384d88b9b1b8924b2.png) depende de si
depende de si  o si
o si 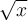 es mayor de 1,5. En caso de que
es mayor de 1,5. En caso de que  , el entero más cercano a
, el entero más cercano a 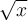 es
es  , por lo que
, por lo que ![[\sqrt{x}] = \sqrt{x}-1 [\sqrt{x}] = \sqrt{x}-1](https://eva.fing.edu.uy/filter/tex/pix.php/d1895b1a19b58388273d8172aaf78295.png) . En caso de que
. En caso de que 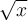 sea mayor a
sea mayor a 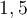 , se tiene que el entero más cercano a
, se tiene que el entero más cercano a 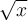 es
es 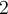 , por lo que
, por lo que ![[\sqrt{x}] = 2-\sqrt{x} [\sqrt{x}] = 2-\sqrt{x}](https://eva.fing.edu.uy/filter/tex/pix.php/f571991132323b0b968ec86d0d148782.png) .
.Por lo tanto, si encontrás en que punto
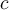 ocurre que
ocurre que  , tenés una fórmula para
, tenés una fórmula para ![[\sqrt{x}] [\sqrt{x}]](https://eva.fing.edu.uy/filter/tex/pix.php/7c6fc2bb16cf68b384d88b9b1b8924b2.png) en el intervalo
en el intervalo ![[1,c] [1,c]](https://eva.fing.edu.uy/filter/tex/pix.php/e7fa0133d10b716aa0dba9dd3d2bccc1.png) y otra para el intervalo
y otra para el intervalo ![[c,4] [c,4]](https://eva.fing.edu.uy/filter/tex/pix.php/c99838766d7fbf2963bea1af3c69d4c8.png) , y en cada caso sabés calcular la integral de la funciones que te quedan (que serían
, y en cada caso sabés calcular la integral de la funciones que te quedan (que serían  en un intervalo y
en un intervalo y  en el otro). Usando la aditividad de la integral, te queda que la integral de
en el otro). Usando la aditividad de la integral, te queda que la integral de ![[\sqrt{x}] [\sqrt{x}]](https://eva.fing.edu.uy/filter/tex/pix.php/7c6fc2bb16cf68b384d88b9b1b8924b2.png) en el intervalo
en el intervalo ![[1,4] [1,4]](https://eva.fing.edu.uy/filter/tex/pix.php/94fe668c80113341416b96929a8f1024.png) es la integral de
es la integral de  de
de  a
a 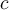 más la integral de
más la integral de  de
de 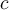 a
a 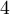 .
.Saludos!