Consultas del libro de ejercicio - Capítulo 3: Integración

Buenas

En este caso tenemos una composición, de una función monótona y la función $[]$ (distancia a el/los entero más cercanos). El hecho de que 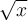$\sqrt{x}$ sea monótona simplifica el problema.

Puedes ver ejemplos similares con la función $\lfloor \rfloor$ Enlace

Vayamos entonces a este ejemplo

Una manera es pensar la función $[x]$ como una función partida. En este caso $\sqrt(x) \in [1,2]$ para todo $x \in [1,4]$ por lo que basta con 2 tramos.

$[x] = \left\lbrace \begin{array}{ll} x-1 & \text{ si } x \in [1,\frac{3}{2}] \\ 2-x & \text{ si } x \in [\frac{3}{2},2]\end{array}\right.$

por lo que la composición pasa a ser

$[\sqrt{x}] = \left\lbrace \begin{array}{ll} \sqrt{x}-1 & \text{ si } \sqrt{x} \in [1,\frac{3}{2}] \\ 2-\sqrt{x} & \text{ si } \sqrt{x} \in [\frac{3}{2},2]\end{array}\right.$

Para $x \in [1,4]$ la condición $\sqrt{x} \in [1,\frac{3}{2}]$ es equivalente a $x \in [1,\frac{9}{4}]$. De forma análoga para $\sqrt{x} \in [\frac{3}{2},2]$ podemos concluir que

$[\sqrt{x}] = \left\lbrace \begin{array}{ll} \sqrt{x}-1 & \text{ si } x \in [1,\frac{9}{4}] \\ 2-\sqrt{x} & \text{ si } x \in [\frac{9}{4},2]\end{array}\right.$

Recuerda que para esta sección ya puedes utilizar cuanto es $\int_{a}^{b} \sqrt{x}dx$

Cualquier cosa vuelve a escribir

Saludos