Hola Alexis.
Sabés que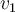 es L.I. con
es L.I. con 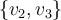 porque son vectores propios asociados a valores propios diferentes.
porque son vectores propios asociados a valores propios diferentes.
Por otra parte, si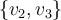 es un conjunto también L.I., entonces
es un conjunto también L.I., entonces 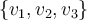 es base de
es base de 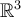 formada por vectores propios. Y esto es independiente de si provienen de un mismo valor propio o no.
formada por vectores propios. Y esto es independiente de si provienen de un mismo valor propio o no.
Acordate de que en teórico vimos ejemplos de transformaciones diagonalizables que tienen "pocos" valores propios pero igual podemos encontrar una base, exactamente como en el ejemplo que preguntaste.
¡Saludos!
Sabés que
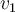 es L.I. con
es L.I. con 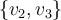 porque son vectores propios asociados a valores propios diferentes.
porque son vectores propios asociados a valores propios diferentes.Por otra parte, si
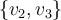 es un conjunto también L.I., entonces
es un conjunto también L.I., entonces 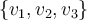 es base de
es base de 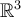 formada por vectores propios. Y esto es independiente de si provienen de un mismo valor propio o no.
formada por vectores propios. Y esto es independiente de si provienen de un mismo valor propio o no. Acordate de que en teórico vimos ejemplos de transformaciones diagonalizables que tienen "pocos" valores propios pero igual podemos encontrar una base, exactamente como en el ejemplo que preguntaste.
¡Saludos!