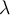Hola, tengo dudas como avanzar en este ejercicio. En la matriz M hallé el polinomio característico y me quedó 
. Entiendo que la sumatoria de multiplicidades algebraicas tiene que ser 3, y además la multiplicidad geometrica para cada vap debe coincidir con la algebraica, pero me quedé trancado en el polinomio.
Agradezco la ayuda
Saludos
Hola Facundo,
Bien! tu razonamiento está correcto, fijate que en el polinomio podés sacar un
de factor común y ahí te va a quedar mejor para estudiar las raíces y sus multiplicidades.
Saludos
Bien! tu razonamiento está correcto, fijate que en el polinomio podés sacar un
de factor común y ahí te va a quedar mejor para estudiar las raíces y sus multiplicidades.Saludos
Bien gracias, ya tengo las 3 raíces, además sé que ![- \sqrt[]{12} \leq a \leq \sqrt[]{12}](https://eva.fing.edu.uy/filter/tex/pix.php/61a16f4855edd6db9826e38ef5f5add8.png "- \sqrt[]{12} \leq a \leq \sqrt[]{12}")
. Cada subespacio propio debe tener dimensión 1, y como prosigo para el cálculo de a?
. Cada subespacio propio debe tener dimensión 1, y como prosigo para el cálculo de a?En realidad el ejercicio no nos pide calcular 
.
Una vez que llegamos a tener un polinomio característico igualado a 0, la idea es estudiar para qué valores de tendremos tres raíces distintas, o si hay valores de para los que hay raíces múltiples, cómo serían en ese caso sus multiplicidades geométricas, etc.
.Una vez que llegamos a tener un polinomio característico igualado a 0, la idea es estudiar para qué valores de
tendremos tres raíces distintas, o si hay valores de para los que hay raíces múltiples, cómo serían en ese caso sus multiplicidades geométricas, etc.Entonces puedo decir que M es diagonalizable ![\forall a: -\sqrt[]{12} \leq a \leq \sqrt[]{12}](https://eva.fing.edu.uy/filter/tex/pix.php/15dcb2a45741b7fbee6a021516cffb0f.png "\forall a: -\sqrt[]{12} \leq a \leq \sqrt[]{12}")
? Aclarando que cuando ![a= \pm \sqrt[]{12}](https://eva.fing.edu.uy/filter/tex/pix.php/09afa1fcf8722cdd74b369777d1abb8a.png "a= \pm \sqrt[]{12}")
existe un valor propio con multiplicidad 2?
Cuando tomo me queda que el subespacio propio tiene dimensión 1, por la tanto no debería considerar ![\pm \sqrt[]{12}](https://eva.fing.edu.uy/filter/tex/pix.php/c4faebe324dcc2646ccf695ebe381773.png "\pm \sqrt[]{12}")
como posibles valores de a, no?
me queda que el subespacio propio tiene dimensión 1, por la tanto no debería considerar como posibles valores de a, no?No estoy segura cómo llegaste a que 
Si sacás el facor común queda
esto es 0 si 
es o 
Si sacás el facor común queda
esto es 0 si es o Bien gracias, tenía un error en las cuentas. Y para este caso todo valor de "a" genera 3 valores distintos, entonces puedo concluir que es diagonalizable?
Sí, es correcto eso