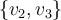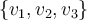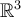Buenas! Tengo una duda puntual sobre el ejercicio:

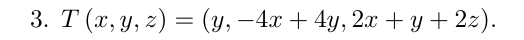
Hallé los valores (raíces) propios de  que son
que son  y una raíz doble que es
y una raíz doble que es 
Es decir, tengo un vector propio 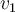 asociado a
asociado a  y dos vectores
y dos vectores  asociados ambos a
asociados ambos a 
Mi duda es: puedo tener una base 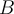 de
de  sabiendo que dos vectores están asociados al mismo valor propio? Me afecta en algo eso a la hora de determinar si los vectores son o no L.I.?
sabiendo que dos vectores están asociados al mismo valor propio? Me afecta en algo eso a la hora de determinar si los vectores son o no L.I.?