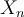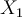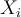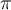Hola. No se me ocurre cómo encontrar la entropía de la parte a)

Lo que hice fue hallar la entropía H(X_1) dado que dice que es uniforme en {0,1}. Luego, pensé en relacionar esa entropía con la de H(X_n) teniendo en cuenta que el proceso es estacionario (se ve en la matriz), pero no encuentro la forma. Si me pueden dar una pista de cómo encontrarla lo agradecería.
Salduos.
Santiago.