Pr.2 Ej6.

Pr.2 Ej6.

de Nicolas Grosso San Roman -
Número de respuestas: 3

Hola! Estoy tratando de hacer la parte a) y b). 

Para la parte a), llegué a que el proceso  \lbrace{X_i}\rbrace es estacionario, pues al ser i.i.d, la probabilidad de que obtenga cierta tira no cambia en el tiempo. Hasta aquí sería correcto? Luego, para terminar de responder esta parte, pensé en encontrar una forma de expresar el proceso  \lbrace{Y_i}\rbrace , y llegué a que:  Y_i = {Y_{i-1} + 1 si X_i = 1 \brace 0 si X_i = 0 } . 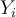Luego de aquí no me resulta tan claro si Y_i es estacionario. Es más, diría que no ya que haciendo algunos casos en mi mente no llego a que las probabilidades de 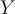Y se igualen en el tiempo. Sin embargo, sí pienso que es de Markov ya que veo que el valor de 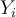Y_i depende del anterior y ninguno más. Hasta aquí que podría mejorar?

Para la parte c) llegué a que la tasa de entropía es H(p) por ser X_i i.i.d.

Y para la parte d) ya no se me ocurre pues no estoy seguro ni de la parte a) y b).

Agradezco la ayuda!!
En respuesta a Nicolas Grosso San Roman

Re: Pr.2 Ej6.

de Maximo Pirri -
Hola,
Buen trabajo. Tu segunda conclusión es la correcta, el proceso no es estacionario pues las probabilidades de Y no se mantienen en el tiempo. Podes incluso pensarlo de forma sencilla con Y1, ¿cuál es la probabilidad de que sea mayor a 1? ¿Se mantiene dicha probabilidad para un Yi genérico?

Tu conclusión para la parte (b) también es correcta, el valor de Yi depende solo del valor anterior (y de Xi). El cálculo de la parte (c) también es correcto.

Para la parte (d) podes usar cualquiera de las dos definiciones de tasa de entropía. Sabiendo que el proceso es de Markov tal vez sea más sencillo usar la segunda definición vista en el curso. También es posible llegar al resultado usando la primera definición, partiendo de la base de que las Yi son función de las Xi. ¿Se cumple también al revés? Ya vimos la relación entre la entropía de una variable aleatoria y una función de ella en el práctico 1, contestando estas preguntas y viendo qué relaciones se cumplen tal vez puedas llegar a la solución con la primera definición.

Saludos.
En respuesta a Maximo Pirri

Re: Pr.2 Ej6.

de Nicolas Grosso San Roman -
Gracias!

Para la primer parte, aún me queda la duda. Yo planteé que P(Y1 = 1) puede ser diferente a P(Yi=1) para algún i diferente de 1. Esto lo veo claro porque P(Y1 = 1) = p, pero que no necesariamente se cumple que P(Y6 =1) = p, ya que esto solo sucede si Y5 = 0 y ese caso no se da siempre.
Esto es suficiente para probar que el proceso no estacionario?
En respuesta a Nicolas Grosso San Roman

Re: Pr.2 Ej6.

de Maximo Pirri -
Buenas,
Lo que dices es correcto y por definición ya pruebas que el proceso no es estacionario. Si te fijas en la definición vista en el curso, la igualdad debe cumplirse para todo n y todo r.
Saludos.