En ambas partes llegué a que los vectores y matrices son linealmente dependientes. ¿Es posible entonces hallar las expresiones generales de las T.L?
Hola Brenda.
Depende, si te fijas en la primera parte tienes que , sin embargo
, sin embargo  por lo que no puede existir una TL tal.
por lo que no puede existir una TL tal.
Depende, si te fijas en la primera parte tienes que
 , sin embargo
, sin embargo  por lo que no puede existir una TL tal.
por lo que no puede existir una TL tal.En la segunda parte no tienes esa incoherencia, pero tienes 4 vectores LD.
Puedes quitar los que sean CL del resto y quedarte con un conjunto LI que no es base de V.
Entonces tienes a T definida sobre un LI que no es base.
La idea es pensar en que podemos hacer cuando tenemos T de un LI que no es base, cómo "rellenar" para poder tener a T definida en todo V.
Saludos
J.
Buenas tardes, tengo una duda respecto a la parte 2 del ejercicio y es que no entiendo cómo hallar 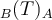 , comprobé que
, comprobé que  sea base (me da que su det es no nulo) pero luego no sé cómo encaminar el asunto.
sea base (me da que su det es no nulo) pero luego no sé cómo encaminar el asunto.
Había considerado tomarme una matriz genérica: pero la verdad es que no creo llegar a ningún lado así.
pero la verdad es que no creo llegar a ningún lado así.
Capaz tenga que hacer algo con la parte 1 pero no creo.
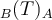 , comprobé que
, comprobé que  sea base (me da que su det es no nulo) pero luego no sé cómo encaminar el asunto.
sea base (me da que su det es no nulo) pero luego no sé cómo encaminar el asunto.Había considerado tomarme una matriz genérica:
 pero la verdad es que no creo llegar a ningún lado así.
pero la verdad es que no creo llegar a ningún lado así.Capaz tenga que hacer algo con la parte 1 pero no creo.
Hola Alexis.
Para armar la matriz pedida, primero calculas  .
.
Esto te da un vector de 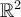 el cual puede escribirse como CL de la base B, o sea que existen dos coeficientes, dos escalares
el cual puede escribirse como CL de la base B, o sea que existen dos coeficientes, dos escalares  .
.
Encuentras dichos coeficientes (que son las coordenadas de 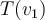 en la base B) y ya tienes la primera columna de la matriz.
en la base B) y ya tienes la primera columna de la matriz.
Repites con 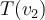 y tienes la segunda columna, etc.
y tienes la segunda columna, etc.
Es aplicar la definición de matriz asociada a una TL.
Saludos
J.
Hola Alexis, creo que tal vez tu confusión venga de que la T no queda determinada por sus valores en los valores que te dan, pues la matrices

No son L.I. ¿puede ser? En ese caso debes ver com ohallar una fórmula general para todas las T posibles, ya que hay muchas. Y luego hacer lo que dice Juan en el mensaje.

No son L.I. ¿puede ser? En ese caso debes ver com ohallar una fórmula general para todas las T posibles, ya que hay muchas. Y luego hacer lo que dice Juan en el mensaje.


