Hola Agustina.
La propiedad está mal definida, puesto que del lado derecho la variable
está cuantificada. Una proposición abierta es una que produce diferentes afirmaciones dependiendo del valor que se sustituya en la(s) variables libres. En este caso la proposición debería ser
.
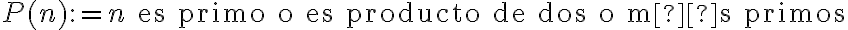En este caso de aplicación del principio de inducción fuerte no es necesario probar ningún paso base, ya que el primer elemento (n = 2) está contemplado en el paso inductivo (es primo y por lo tanto se cumple la tesis inductiva).
Cuando aplicamos el principio de inducción fuerte, la diferencia clave con el principio de inducción simple es que en la hipótesis inductiva no sólo suponemos que la propiedad se cumple para un elemento dado si no que suponemos que se cumple para todos los elementos desde el primero que consideramos hasta uno dado, y a partir de eso probamos que necesariamente la propiedad se tiene que cumplir para el siguiente.
Teniendo eso en cuenta la hipótesis inductiva en este caso es que dado n mayor o igual a 2 fijo, para todo k mayor o igual a 2 y menor estricto que n se cumple P(k) y la tesis es que se cumple P(n).
Por ejemplo, si n fuera 2, la hipótesis dice que para todos los k mayores o iguales a 2 y menores estrictos que 2 se cumple P(k) (y fijate que como no hay ningún k que cumpla ambas condiciones en simultáneo, la hipótesis no nos dice nada, o sea pasa lo mismo que si lo tomáramos como un paso base) y la tesis dice que se cumple P(2). Ahora si n fuera 8, la hipótesis dice que se cumple para 2,3,4,5,6 y 7, y la tesis dice que se cumple para 8.
Tu prueba del paso inductivo está esencialmente bien (una vez arreglada la hipótesis inductiva). Lo único que habría que justificar con un poco más de detalle es por qué a y b son menores a k. Lo necesario es probar que son menores o iguales a k, pero ambas afirmaciones son ciertas en este caso puntual. Una forma fácil de verlo es que si alguno de los dos fuera mayor o igual a k+1, como a su vez ambos son mayores o iguales a 2 por ser divisores propios, el producto que es k+1 sería mayor o igual a 2(k+1) de lo cual se deduce que 1 sería mayor o igual a 2 y eso es absurdo.
Por último, es necesario aclarar en la conclusión que la aplicación del principio de inducción fuerte es válida porque se verificaron sus hipótesis que son el paso base y el paso inductivo sobre la propiedad definida. Esto es lo mismo que te expliqué en el otro ejercicio así que no lo voy a repetir acá.
Si te quedó alguna duda de mi explicación no dudes en volver a preguntar.
Saludos,
Gabriel
La propiedad está mal definida, puesto que del lado derecho la variable
está cuantificada. Una proposición abierta es una que produce diferentes afirmaciones dependiendo del valor que se sustituya en la(s) variables libres. En este caso la proposición debería ser 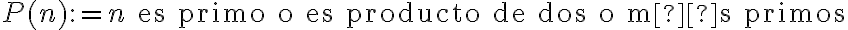.En este caso de aplicación del principio de inducción fuerte no es necesario probar ningún paso base, ya que el primer elemento (n = 2) está contemplado en el paso inductivo (es primo y por lo tanto se cumple la tesis inductiva).
Cuando aplicamos el principio de inducción fuerte, la diferencia clave con el principio de inducción simple es que en la hipótesis inductiva no sólo suponemos que la propiedad se cumple para un elemento dado si no que suponemos que se cumple para todos los elementos desde el primero que consideramos hasta uno dado, y a partir de eso probamos que necesariamente la propiedad se tiene que cumplir para el siguiente.
Teniendo eso en cuenta la hipótesis inductiva en este caso es que dado n mayor o igual a 2 fijo, para todo k mayor o igual a 2 y menor estricto que n se cumple P(k) y la tesis es que se cumple P(n).
Por ejemplo, si n fuera 2, la hipótesis dice que para todos los k mayores o iguales a 2 y menores estrictos que 2 se cumple P(k) (y fijate que como no hay ningún k que cumpla ambas condiciones en simultáneo, la hipótesis no nos dice nada, o sea pasa lo mismo que si lo tomáramos como un paso base) y la tesis dice que se cumple P(2). Ahora si n fuera 8, la hipótesis dice que se cumple para 2,3,4,5,6 y 7, y la tesis dice que se cumple para 8.
Tu prueba del paso inductivo está esencialmente bien (una vez arreglada la hipótesis inductiva). Lo único que habría que justificar con un poco más de detalle es por qué a y b son menores a k. Lo necesario es probar que son menores o iguales a k, pero ambas afirmaciones son ciertas en este caso puntual. Una forma fácil de verlo es que si alguno de los dos fuera mayor o igual a k+1, como a su vez ambos son mayores o iguales a 2 por ser divisores propios, el producto que es k+1 sería mayor o igual a 2(k+1) de lo cual se deduce que 1 sería mayor o igual a 2 y eso es absurdo.
Por último, es necesario aclarar en la conclusión que la aplicación del principio de inducción fuerte es válida porque se verificaron sus hipótesis que son el paso base y el paso inductivo sobre la propiedad definida. Esto es lo mismo que te expliqué en el otro ejercicio así que no lo voy a repetir acá.
Si te quedó alguna duda de mi explicación no dudes en volver a preguntar.
Saludos,
Gabriel