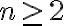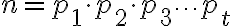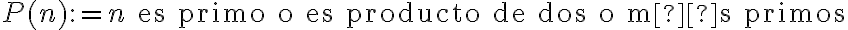Buenas!, Quería consultar acerca de si mi planteamiento está bien
Fue muchísimo más teórico que práctico, ya que el ejercicio al decir específicamente 
Se me ocurrió que era mejor comprobar la existencia de los números compuestos, y como los primos solo podían ser productos de sí mismo y 1, lo que se contrapone a la definición de compuesto la cual da como definición que 1<D<N, con N el producto de un número diferente de 1, y de sí mismo.
Como paso base utilice los 3 primeros números primos, [2, 3, 5], el cual plantee que ya infiere que estos contraponen a la definición de compuesto, ya que está siendo expresado como un producto de sí mismo y 1, y por definición ya lo está contradiciendo.
Como HI indiqué que existía entonces un compuesto perteneciente a los naturales, el cual se podía expresar como producto de sí mismo y 1.
Como TI indiqué la única forma de que N=m*p sean iguales a N, es que N=m ó N=p, y que m o p sean iguales a 1 (no simultáneamente), lo cual contradice a la definición de número compuesto, ya que N>M>P, con P=1, por lo tanto N≠M, y N≠P, a lo que llegué es que no existe un número compuesto el cual se pueda expresar como producto de si mismo y 1, lo cual contradice a mi hipótesis inductiva.
Quisiera saber si tuve algún error de planteo, o de reiteración, o si de por sí la lógica aplicada está mal, saludos.