|
Hola, ¿qué tal? Quisiera saber si la demostración que adjunto cumple con los estándares necesarios y si hay aspectos en los que podría mejorarla. Agradezco cualquier sugerencia o comentario. |

|
Hola, ¿qué tal? Quisiera saber si la demostración que adjunto cumple con los estándares necesarios y si hay aspectos en los que podría mejorarla. Agradezco cualquier sugerencia o comentario. |

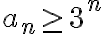 se cumple para todos los valores mayores o iguales que 1, pero repetidamente escribís que vas a probar que se cumple
se cumple para todos los valores mayores o iguales que 1, pero repetidamente escribís que vas a probar que se cumple 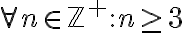 . Lo primero es que después del cuantificador universal "para todo" nunca va dos puntos. Si se quiere decir "para todo elemento que cumpla x condición" se puede hacer con palabras, pero el uso de los cuantificadores como sufijos (es decir después de la afirmación que cuantifican) ya es un abuso de notación en sí mismo. La forma correcta de hacer tal afirmación si se quisiera (cosa que de nuevo, no es lo que pide este ejercicio pero aprovecho la oportunidad para explicarlo) sería
. Lo primero es que después del cuantificador universal "para todo" nunca va dos puntos. Si se quiere decir "para todo elemento que cumpla x condición" se puede hacer con palabras, pero el uso de los cuantificadores como sufijos (es decir después de la afirmación que cuantifican) ya es un abuso de notación en sí mismo. La forma correcta de hacer tal afirmación si se quisiera (cosa que de nuevo, no es lo que pide este ejercicio pero aprovecho la oportunidad para explicarlo) sería 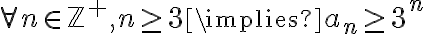 .
. al principio pero lo que sigue no es una proposición abierta (es decir con una variable
al principio pero lo que sigue no es una proposición abierta (es decir con una variable 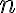 indeterminada) porque justamente la cuantificaste. La proposición en este caso debería ser
indeterminada) porque justamente la cuantificaste. La proposición en este caso debería ser 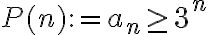 .
.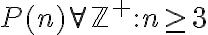 acá además de la aclaración que ya hice arriba directamente pusiste un cuantificador sin ninguna variable que cuantifique. El punto clave acá es que los símbolos matemáticos no son sólo atajos para escribir palabras. Tienen un significado muy preciso y bien definido, y con ello un uso limitado.
acá además de la aclaración que ya hice arriba directamente pusiste un cuantificador sin ninguna variable que cuantifique. El punto clave acá es que los símbolos matemáticos no son sólo atajos para escribir palabras. Tienen un significado muy preciso y bien definido, y con ello un uso limitado.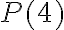 lo cual contradice lo que dijiste más arriba, ya que si lo fueras a probar para todo entero mayor o igual que 3 tu paso base debería consistir en probarlo para 3.
lo cual contradice lo que dijiste más arriba, ya que si lo fueras a probar para todo entero mayor o igual que 3 tu paso base debería consistir en probarlo para 3.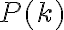 y
y 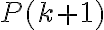 . Para eso es que se define una vez al principio. Dicho esto si la definición es la que dije más arriba (que es lo que se infiere de lo que escribiste) lo que decís en la hipótesis inductiva que debería ser
. Para eso es que se define una vez al principio. Dicho esto si la definición es la que dije más arriba (que es lo que se infiere de lo que escribiste) lo que decís en la hipótesis inductiva que debería ser 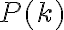 está mal, puesto que la afirmación debería ser sobre
está mal, puesto que la afirmación debería ser sobre 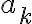 y no
y no 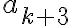 . En la tesis inductiva pasa algo peor porque
. En la tesis inductiva pasa algo peor porque 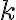 no cambia del lado izquierdo de la desigualdad pero sí del lado derecho.
no cambia del lado izquierdo de la desigualdad pero sí del lado derecho.