Si hacés el límite de la sucesión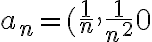 
y da distinto de 
entonces no existe el límite, porque tenés dos resultados distintos al acercarte de dos formas distintas (la de esa parábola y la de cualquier recta). Si el límite da no nos dice nada, porque podría haber otra forma de acercarte que de distinto de , puede ser otra parábola u otra curva de orden mayor por ejemplo. Una herramienta para intentar probar que sí es sería estudiar con polares y utilizar la propiedad del ejercicio 4 del práctico 7 (tal vez ahí vale la pena antes hacer un cambio de variable $$y^2 = u)
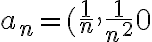y da distinto de entonces no existe el límite, porque tenés dos resultados distintos al acercarte de dos formas distintas (la de esa parábola y la de cualquier recta). Si el límite da no nos dice nada, porque podría haber otra forma de acercarte que de distinto de , puede ser otra parábola u otra curva de orden mayor por ejemplo. Una herramienta para intentar probar que sí es sería estudiar con polares y utilizar la propiedad del ejercicio 4 del práctico 7 (tal vez ahí vale la pena antes hacer un cambio de variable $$y^2 = u)