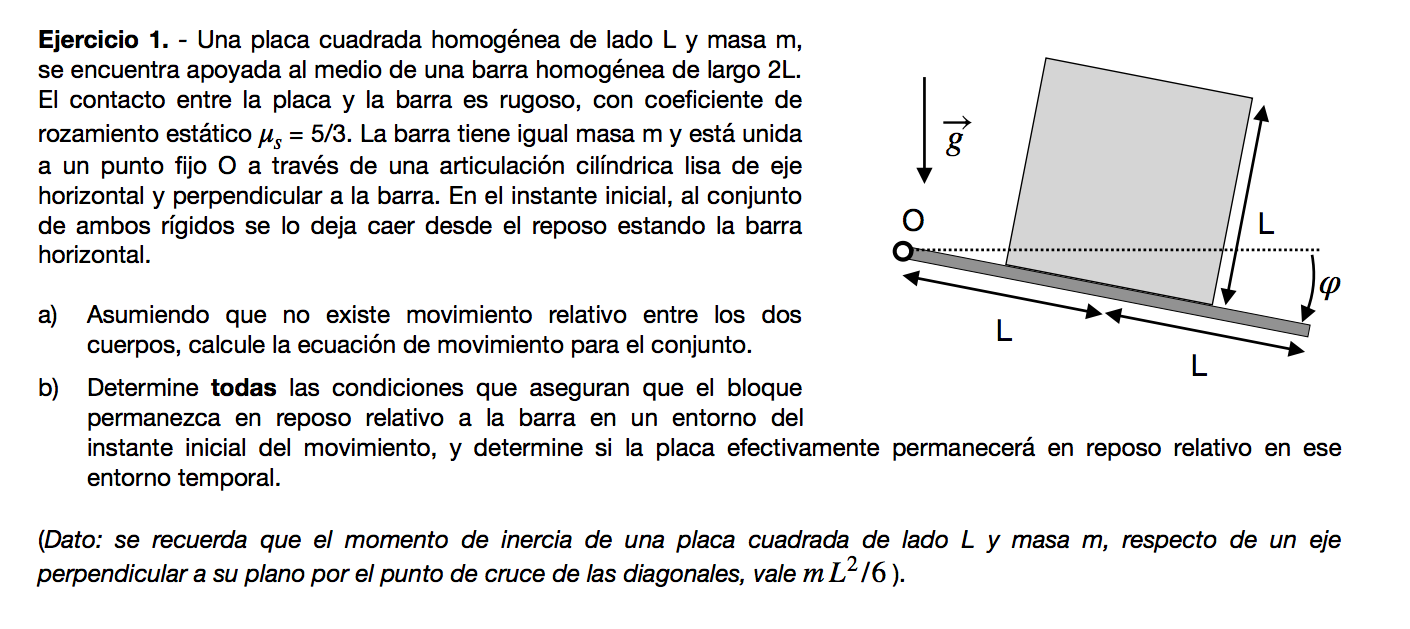
Buenas tardes. Me surgieron varias dudas haciendo este parcial, en el ejercicio 1.
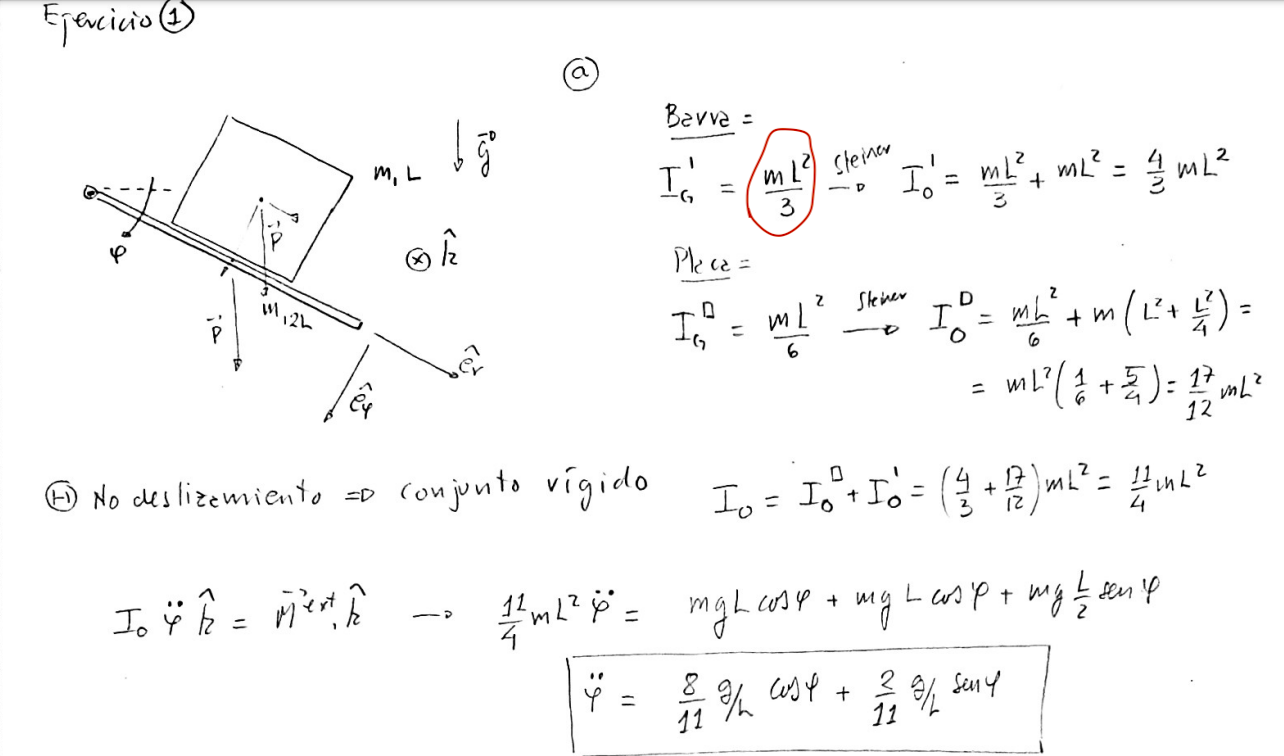
1) Tenía el dato de que la inercia de una barra respecto a su cm es ML²/12, pero acá usan ML²/3. Me pareció raro, y ya me pasó algo similar con el parcial de 2023, por lo que no sé si tengo los datos mal o estoy interpretando mal las soluciones.
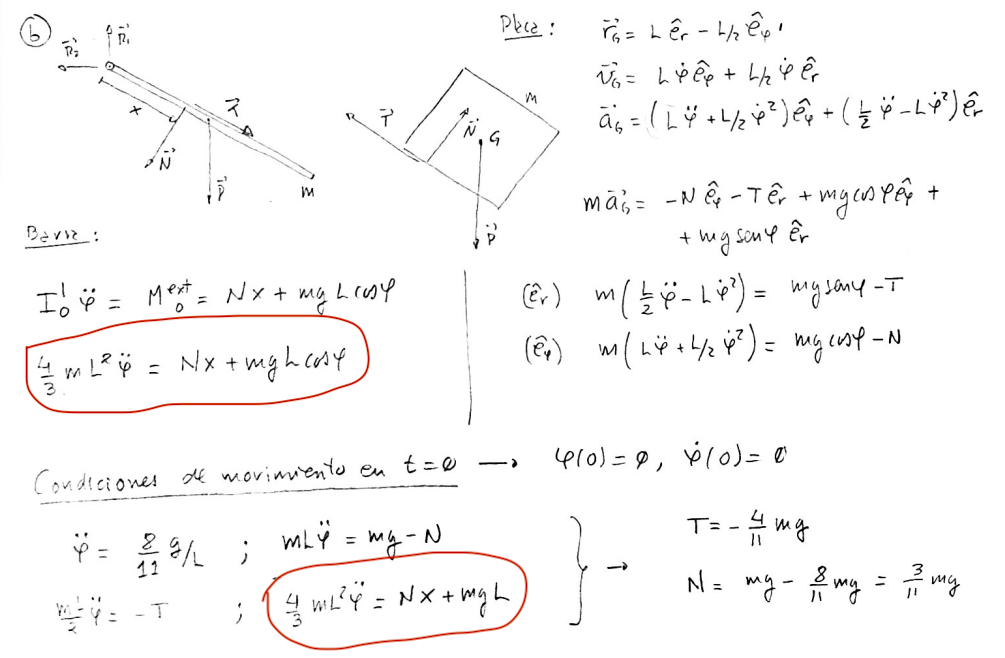
2) Al hacer los momentos respecto de O, pensé en la articulación cilíndrica. En esta hay reacciones y también un Momento(articulación/barra), por lo que pensé que tenía que ponerlo en la suma de momentos. Vi que en la solución no lo ponían, y pensé que a lo mejor es porque se está calculando el momento desde O. Sin embargo me acordé de que en equilibrio cuando hay por ejemplo un empotramiento, existe un momento entre la pared y la viga pero si calculamos la suma de momentos desde ese punto se considera igual, por lo que no entiendo muy bien el criterio de cuándo ponerlo. (En ejercicios de pr6 y pr8 donde hay articulaciones cilídricas no los he puesto y estaba bien pero no me cuestioné por qué).
3) Por último, en la parte b), para hallar las condiciones de equilibrio relativo hace el diagrama de cuerpo libre de los dos rígidos y utiliza la barra para despejar x. Pero ¿podría haber hecho todo con las cardinales de la placa?. Intenté y me dio cualquier cosa pero no sé si es error de cuentas y seguir intentando o tengo mal algún concepto.
Agradezco si me pueden aclarar alguna!