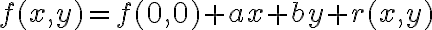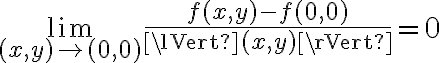Buenas, tengo una duda de la resolución de este ejercicio. Al ver si la f es diferenciable, utiliza la definición y tenia entendido que para usar las derivadas parciales en la definición de diferenciabilidad se tiene que comprobar si son continuas en el punto, en este caso en (0,0) pero en la solución no se planteo eso, sino que se usaron directamente.
yo había planteado esto para ver si la derivada parcial en x es continua pero me surgió esta duda de el limite, ya que si utilizo diferentes rectas me queda distinto. en x=0 me queda continua pero en el otro no. Desde ya muchas gracias