Buenas tardes, tengo una duda respecto a este ejercicio:
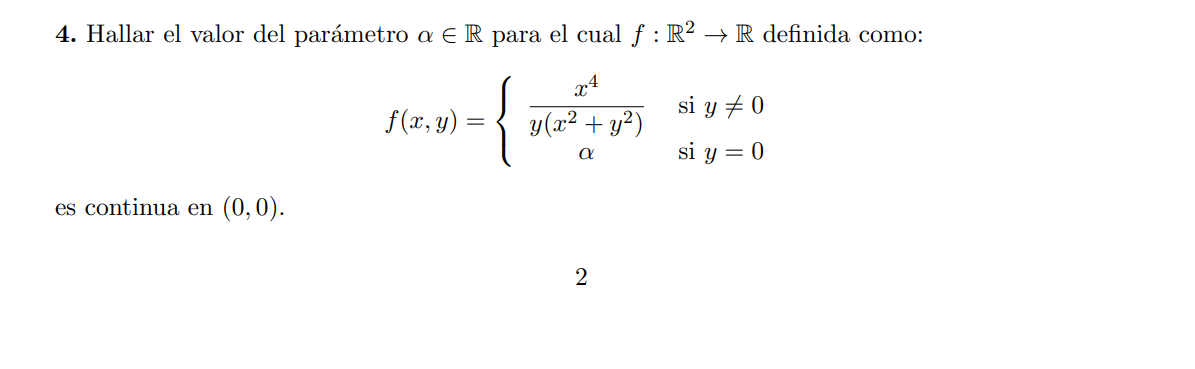

Si aplico polares para determinar la existencia del límite cuando 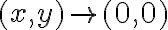 me queda que el límite da
me queda que el límite da  y en todo caso
y en todo caso 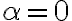 para que
para que 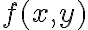 sea continua. También apliqué límite direccional acercándome por la recta
sea continua. También apliqué límite direccional acercándome por la recta 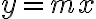 y me da nuevamente el mismo valor para
y me da nuevamente el mismo valor para  (si es que dicho límite existe)
(si es que dicho límite existe)
Pero si me acerco por la curva 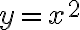 me queda como numerador
me queda como numerador  que no existe. Entonces diría que es la
que no existe. Entonces diría que es la 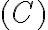 por esa razón.
por esa razón.
Pero mi duda es la siguiente: para determinar la existencia (o no existencia) de límites usamos coordenadas polares, pero para éste método existe el 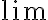 y vale
y vale  , ¿entonces por qué la opción
, ¿entonces por qué la opción  es errónea?
es errónea?

