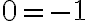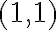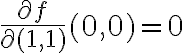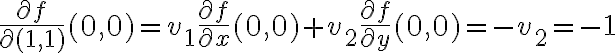CDIVV-2S: Examen Febrero 2022 (DESARROLLO parte c) | FING

Página Principal

Examen Febrero 2022 (DESARROLLO parte c)

Buenas, no entiendo lo siguiente para este ejercicio:

En la parte

$c$ se quiere determinar la diferenciabilidad de

$f$ y se concluye que no lo es a través de un absurdo, más precisamente:

Lo que no comprendo eso lo siguiente:
Estamos parados en la ecuación resultante sobre las derivadas direccionales,

$v_2 \frac{v_1 ^2 - v_2 ^2}{v_1 ^2 + v_2 ^2}$
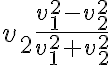
Comprendo que para

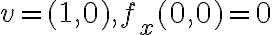$v=(1,0) , f_x (0,0)=0$ y

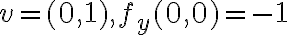$v=(0,1) , f_y (0,0)=-1$ entonces queda como resultado (por el Teorema)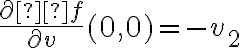

$\frac{\partial f }{\partial v} (0,0)=-v_2$

Luego, para

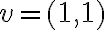$v=(1,1)$ se tiene que

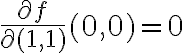$\frac{\partial f }{\partial (1,1)} (0,0)=0$ pero no entiendo por qué de esa misma derivada se tiene que es igual a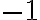

$-1$
porque ahí

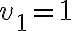$v_1 = 1$ y

$v_2 = 1$ y

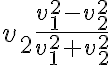$v_2 \frac{v_1 ^2 - v_2 ^2}{v_1 ^2 + v_2 ^2}$ siempre te da

$0$

No veo de dónde se llega a la contradicción

$0=-1$

Re: Examen Febrero 2022 (DESARROLLO parte c)

de Leandro Bentancur - jueves, 23 de noviembre de 2023, 13:57

Buenas,
Por el cálculo de la derivada direccional en la dirección

$(1,1)$ obtenés

$\frac{\partial f}{\partial (1,1)} (0,0)=0$ como decís. Luego si la función fuera diferenciable tendríamos que

$\frac{\partial f}{\partial (1,1)} (0,0)= v_1 \frac{\partial f}{\partial x} (0,0) + v_2 \frac{\partial f}{\partial y} (0,0) = -v_2 = -1$ , y ahí está la contradicción.
Saludos,
Leandro