Buenas,
Queria saber si mis graficos estan bien hechos, me costo entender los dominios:
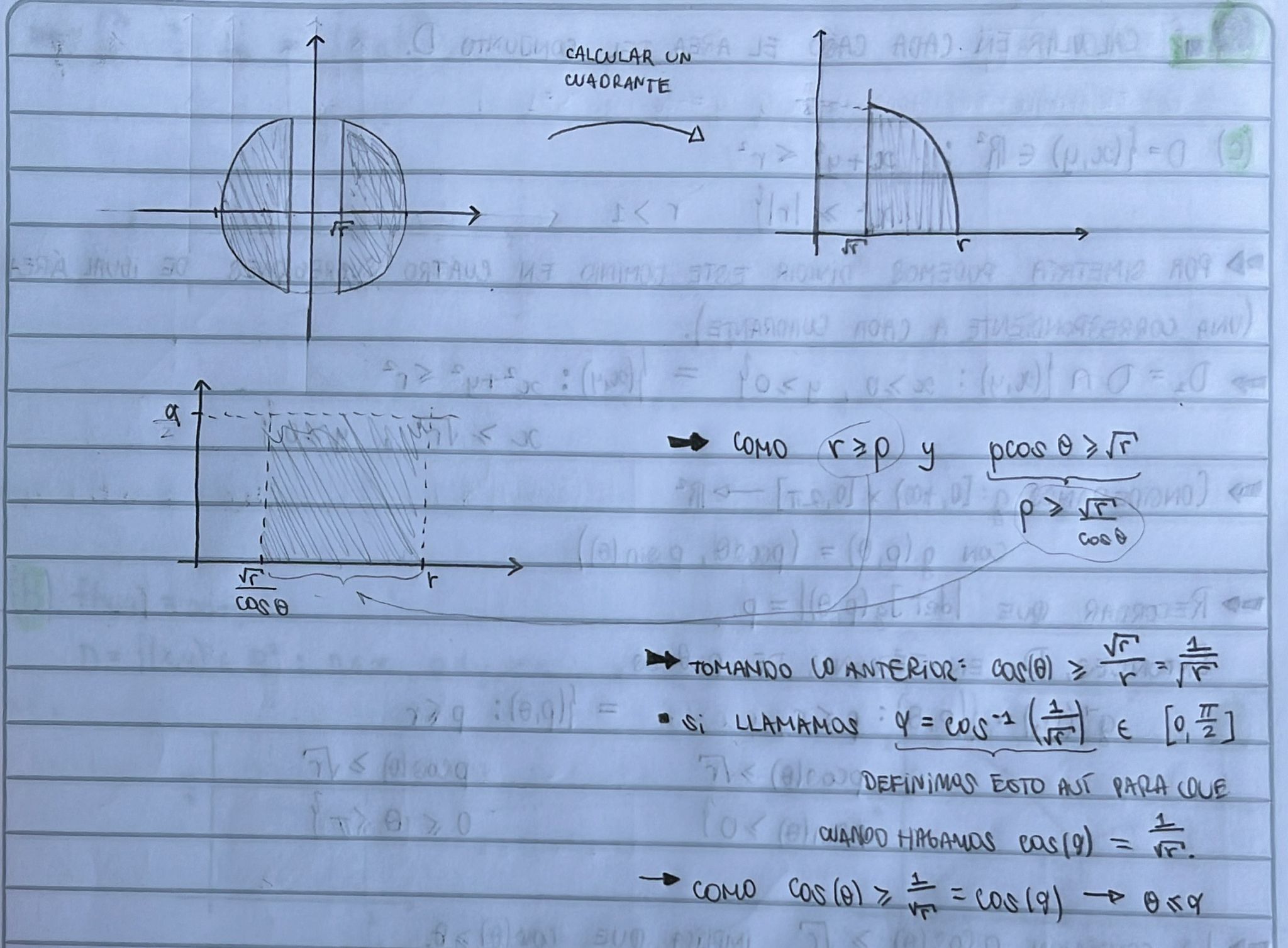
Buenas,
Queria saber si mis graficos estan bien hechos, me costo entender los dominios:

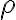 y
y  sirve para expresar de alguna forma los límites de integración de ese primer cuadrante pero el borde de la izquierda no es una recta vertical, aclaro por las dudas. De hecho esa curva comienza en
sirve para expresar de alguna forma los límites de integración de ese primer cuadrante pero el borde de la izquierda no es una recta vertical, aclaro por las dudas. De hecho esa curva comienza en 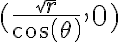 y termina en el punto
y termina en el punto 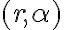 .
. en el dominio indicado.
en el dominio indicado. 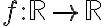 que tiene valores positivos y negativos, por ejemplo
que tiene valores positivos y negativos, por ejemplo 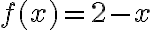 en el intervalo
en el intervalo ![[0,3] [0,3]](https://eva.fing.edu.uy/filter/tex/pix.php/ed9c05fe24c0f49f5d73f494a921e0c4.gif) , la integral allí resulta el área del triángulo definido entre el eje y el gráfico en la región que es positiva (
, la integral allí resulta el área del triángulo definido entre el eje y el gráfico en la región que es positiva (![[0,2] [0,2]](https://eva.fing.edu.uy/filter/tex/pix.php/70fd3f388413505934da60b43afc4088.gif) ) menos el área del triángulo definido entre el eje y el gráfico en la región que es negativa (
) menos el área del triángulo definido entre el eje y el gráfico en la región que es negativa (![[2,3] [2,3]](https://eva.fing.edu.uy/filter/tex/pix.php/d5138fec13c27bb6c645b29cdfa97a84.gif) ). En definitiva, la integral de un función positiva equivale a un área (o volumen) de una región entre el gráfico y el subespacio correspondiente al dominio, y la integral de una función negativa corresponde a la integral de la parte positiva restada por la integral de la parte negativa. No sé si ayuda a esclarecer mejor este párrafo pero ante la duda lo importante es lo que mencioné en el primer párrafo.
). En definitiva, la integral de un función positiva equivale a un área (o volumen) de una región entre el gráfico y el subespacio correspondiente al dominio, y la integral de una función negativa corresponde a la integral de la parte positiva restada por la integral de la parte negativa. No sé si ayuda a esclarecer mejor este párrafo pero ante la duda lo importante es lo que mencioné en el primer párrafo.