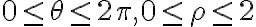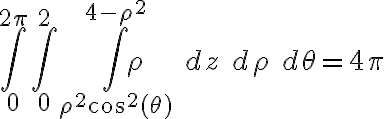Buenas, utilice el cambio de variables a coordenadas polares g(ρ,θ,z)=(ρcos(θ),ρsen(θ),z) , y mi planteo fue que como tengo que calcular el volumen encerrado entre z = x^2 ,y z= 4 - x^2 - y^2, entonces la figura la podia representar como x^2 ≤ z ≤ 4 - x^2 - y^2, entonces al hacer el cambio de variable en esta ecuacion, llego a que ρ ≤ √( 4/(1+cos(θ)^2) ) , entonces yo hice la integral, integral[0,4] integral[0,2π] integral[0,√( 4/(1+cos(θ)^2) )] ρ dρ dθ dz , y todo esto me dio (8√2)π, que es parecido al resultado de las soluciones pero no es el mismo, donde estaria mi error?
Buenas Ticciano,
Estoy de acuerdo con que tenés que hacer el cambio de variable en las ecuaciones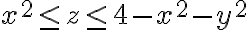 
pero no entendí cómo llegaste a 
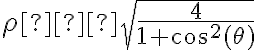. Además tenés dos desigualdades por lo que deberías obtener dos desigualdades de nuevo. Te animás a revisar esa parte a ver si arreglando ahí sale? Sino escribime nuevamente explicándome qué pasos seguiste para llegar a esa desigualdad.
Saludos,
Leandro
como x^2 ≤z ≤ 4−x^2−y^2 entonces x^2 ≤ 4−x^2−y^2 , al hacer el cambio de variable me queda (ρcos(θ))^2 ≤ 4 - (ρcos(θ))^2 - (ρsen(θ))^2 = 4 - ρ^2 , entonces ahi hice el despeje. Lo de trabajar las dos desigualdades por separado no probe, pero igual quisiera entender cual es el error de lo que hice
Las desigualdades que limitan el conjunto son ambas, por lo que tenemos que utilizar las dos en el cambio de variable. La desigualdad que obtuviste no determina el conjunto, por ejemplo tenés que 
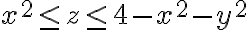no está acotado usando esa sola. Habría que hacer el cambio de variable en (podés escribir las dos por separado también, es lo mismo).
Cualquier cosa volvé a escribir nomás y seguimos.
Saludos,
Leandro
no está acotado usando esa sola. Habría que hacer el cambio de variable en 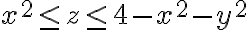(podés escribir las dos por separado también, es lo mismo). Cualquier cosa volvé a escribir nomás y seguimos.
Saludos,
Leandro
Buenas, resolví el ejercicio pero llegué a un resultado distinto al de la resolución y no veo dónde está el error.
Al hacer el cambio de variable a cilíndricas, lo que intenté fue recorrer el circunferencia de centro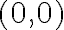 
y radio 
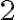, pues es la interseccion del paraboloide con el plano del suelo, y luego hacer variar 
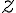tal que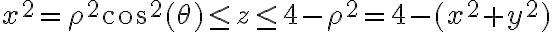 
También tengo, 
y esto se convierte en la integral
Hola Ezequiel,
Si observás los gráficos de las funciones, al proyectar la intersección del paraboloide y el gráfico de la función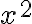
en las variables 
e 
no obtenemos toda la circunferencia de centro 
y radio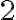 
. Esta restricción la podés obtener de 
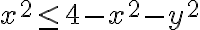(y luego transformarla a polares), lo que te da una restricción de 
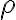en función de 
.
Saludos,
Leandro
Si observás los gráficos de las funciones, al proyectar la intersección del paraboloide y el gráfico de la función
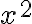en las variables e no obtenemos toda la circunferencia de centro y radio 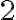. Esta restricción la podés obtener de 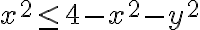(y luego transformarla a polares), lo que te da una restricción de 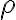en función de .Saludos,
Leandro