Buenas, tenia una duda de como saber si la función dependiendo de ϴ es acotada o no. en este ejercicio me quedo de esta forma la función, y no se como darme cuenta si esta acotada para así aplicar la propiedad de que como p tiende a 0 y la función dependiente de ϴ es acotada, el limite es 0. Muchas gracias
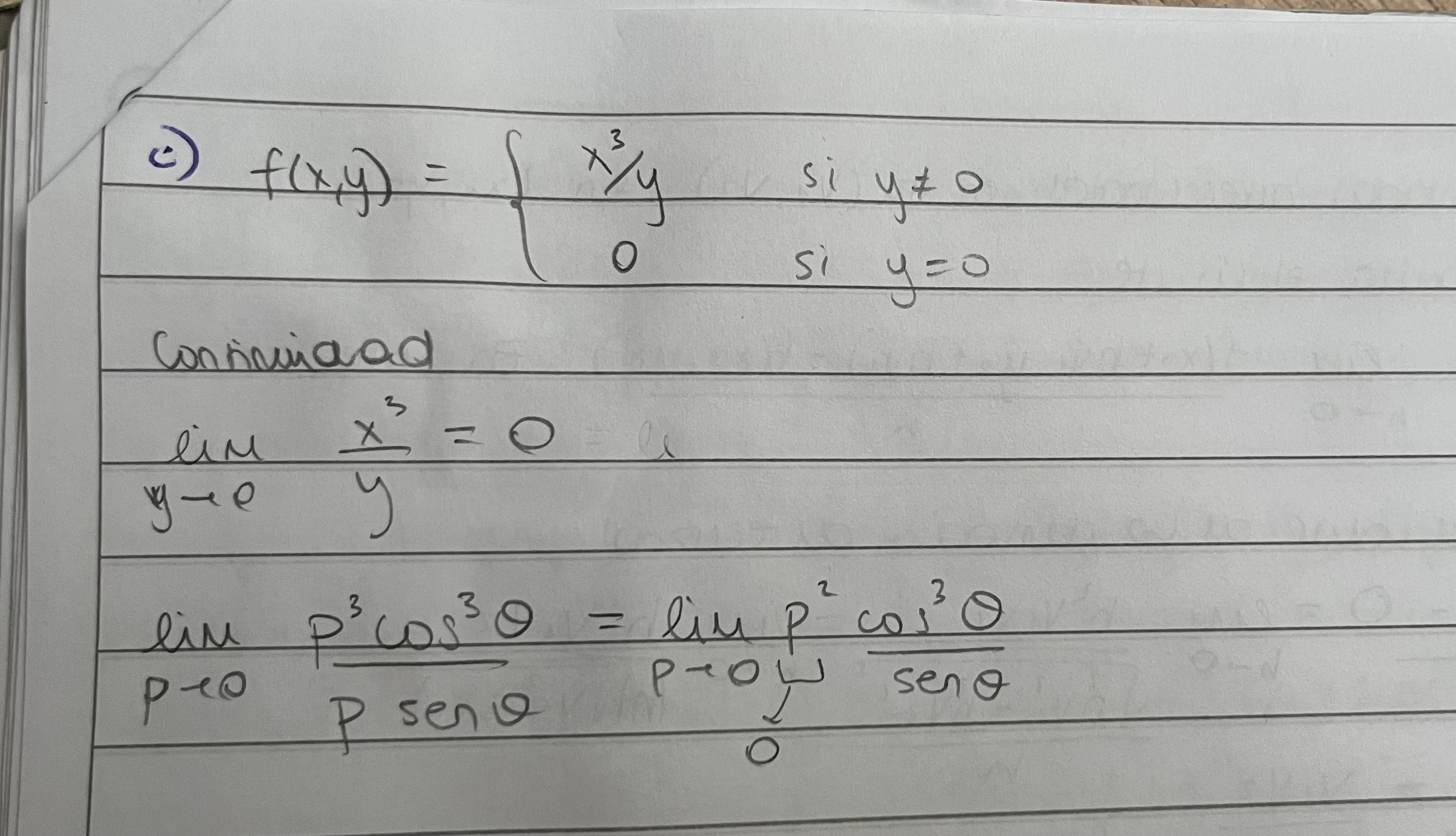




![[0,2 \pi] [0,2 \pi]](https://eva.fing.edu.uy/filter/tex/pix.php/bc12eaeab36df1cd0b20123a762db79c.gif)