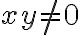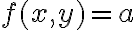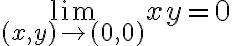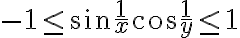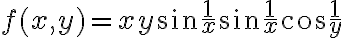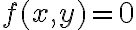Buenas! Me preguntaba si era válido usar los polinomios de taylor para las funciones seno y coseno que menciona ahi como hacíamos en el curso pasado, ahi quedaria bastante mas simple la resolucion del límite pero bueno como es en varias variables quizás es diferente. Gracias!
Hola Sol,
El ejercicio te pide estudiar la continuidad y existencia de derivadas direcionales a la funciòn:
Notar que si 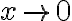 entonces
entonces 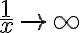 por lo que Taylor no es el enfoque adecuado.
por lo que Taylor no es el enfoque adecuado.
En este caso, podes usar el hecho que el las funciones seno y coseno son acotadas y que el limite del producto de una funcion que tiende a cero por una acotada es cero.
Por ejemplo estudiemos, primero la continuidad en  para determinar
para determinar  :
:
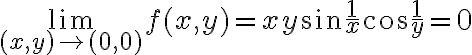 , como
, como 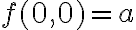 para que
para que  sea continua en
sea continua en  ,
, 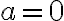 .
.
Luego la función toma la forma:
Habria que:
- Estudiar conrtinuidad para los puntos de la forma
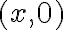 con
con 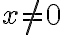 (eje 0x) y los puntos
(eje 0x) y los puntos 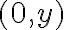 con
con  diferente de
diferente de  (eje 0y)
(eje 0y) - Estudiar las derivadas direccionales cuando
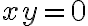 , también te sugiero separar el caso
, también te sugiero separar el caso  , luego el eje 0x y el eje 0y
, luego el eje 0x y el eje 0y
Espero que puedas avanzar...
lo que ocurre para la recta x=0 es que si y tiende a cualquier punto de todas maneras el límite me da 0, el conflicto lo encuentro únicamente cuando hago tender a y por ejemplo a mas infinito utilizando la curva 1/x para y, el tema es que no se si eso tiene sentido alguno porque el infinito no vendría a ser un "punto" en el dominio, por lo que analizar ahí la continuidad me resulta un poco absurdo.