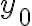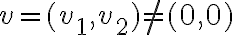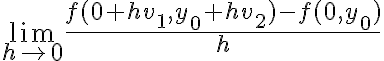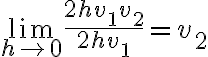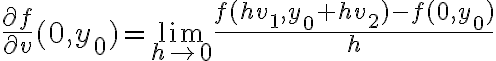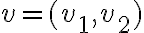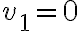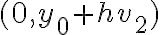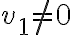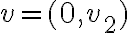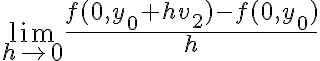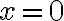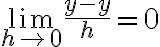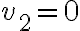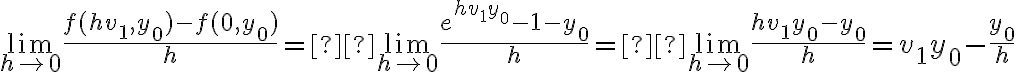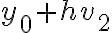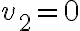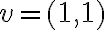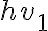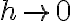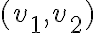Ej 4)b

Ej 4)b

de Bruno Scanziani Etchebarne -
Número de respuestas: 11

Hola,cuando voy a hacer el límite para la derivada, no se si tengo que calcularlo como

f(0+h,y) - f(0,y) /h o si tengo que hacerlo dos veces poniendo: f(0+h,y) -f(0,0) / h y f(x,0+h) - f(0,0) / h.

El problema principal es que no se de que forma escribir el limite


En respuesta a Bruno Scanziani Etchebarne

Re: Ej 4)b

de Florencia Uslenghi -

Hola Bruno!

En este parte pide calcular las derivadas direccionales entonces lo que hay que calcular es el límite, fijando un y_0 y definiendo un vector de dirección v=(v_1,v_2)\neq(0,0):

\lim_{h \rightarrow 0} \frac{f(0+hv_1, y_0+hv_2)-f(0,y_0)}{h}

Si tenés más dudas de cómo calcular el límite volvé a escribir :)

Saludos!

Florencia
En respuesta a Florencia Uslenghi

Re: Ej 4)b

de Ignacio Hereu Carnebale -
Buenas, haciendo el 4.b) el limite me dio como resultado \lim_{h\to 0} \frac{2hv_{1}v_{2}}{2hv_{1}}=v_{2} 
Con este resultado, ya puedo asumir que existen las derivadas direccionales para cualquier dirección?
Saludos.
En respuesta a Ignacio Hereu Carnebale

Re: Ej 4)b

de Florencia Uslenghi -
Buenas!
Sí! Con ese resultado podemos afirmar que existe, el problema estaría si el límite no existiera o no fuera finito.
Saludos,
Florencia
En respuesta a Florencia Uslenghi

Re: Ej 4)b

de Alexis Sokorov Vargas -
Buenas, no entiendo cómo representar \frac{\partial f}{\partial v} (0,y_0)= \lim_{h \to 0} \frac{ f(hv_1 , y_0 + hv_2) - f(0,y_0)}{h}
En respuesta a Alexis Sokorov Vargas

Re: Ej 4)b

de Leandro Bentancur -
Buenas Alexis,

Para calcular el límite el siguiente paso es sustituir por los valores funcionales y tendríamos dos casos. Si v=(v_1,v_2), un caso es cuando v_1=0 porque ahí los puntos (0,y_0+hv_2) donde estamos evaluando la f se comportan como la función y, y el otro cuando v_1 \neq 0 porque ahí la función se comporta como \frac{e^{xy}-1}{x}. Una vez que hacemos la sustitución, calculamos el límite con h tendiendo a 0.

Si tenés alguna otra duda al continuar haciendo el ejercicio volvé a escribir nomás.

Saludos!
En respuesta a Leandro Bentancur

Re: Ej 4)b

de Alexis Sokorov Vargas -
Buenas tengo dos dudas:
1) Si considero el vector v=(0,v_2) me queda el siguiente límite: \lim_{h \to 0} \frac{ f(0, y_0 + hv_2) - f(0, y_0)}{h} que, según cómo está definida f en el primer miembro del numerador me queda y y en el segundo también, porque cuando x=0 la función te tira y, no? Entonces sería \lim_{h \to 0} \frac{y-y}{h} = 0 

2) cuando v_2 = 0 , \lim_{h \to 0} \frac{f(hv_1, y_0)-f(0,y_0)}{h}= \lim_{h \to 0} \frac{e^{hv_1 y_0} - 1 - y_0}{h} = \lim_{h \to 0} \frac{hv_1 y_0 - y_0}{h} = v_1 y_0 - \frac{y_0}{h} entonces ahí se me complica o no sé si se hace así
En respuesta a Alexis Sokorov Vargas

Re: Ej 4)b

de Leandro Bentancur -
Hola Alexis,
1) La idea está bien, pero en el primer sumando del numerador te queda y_0+hv_2 y en el segundo te queda y_0, por lo que el resultado queda distinto.
2) El caso complementario al primero es cuando v_1 \neq 0, si imponés que v_2=0 entonces te están faltando la mayoría de las direcciones, por ejemplo v=(1,1). Cuando sustituís te faltó dividir por x, que en este caso sería hv_1, ahí te va a quedar que el límite sí existe. En la última igualdad no podemos evaluar aún, porque h es una variable dentro del límite. Si te quedara así al tomar el límite con h \to 0 entonces el límite no existiría.
Saludos,
Leandro
En respuesta a Leandro Bentancur

Re: Ej 4)b

de Marcos Dura Sosa -
Buenas,

No entiendo porque harias el caso 2) si florencia en este hilo dijo que con calcular el limite de (0,y0) con el resultado que es V2 ya podiamos concluir que existen todas las direccionales. 

Muchas gracias.
En respuesta a Marcos Dura Sosa

Re: Ej 4)b

de Leandro Bentancur -
Hola Marcos,

Florencia comentó que la existencia de ese límite (y que sea finito) es que exista la derivada direccional. Mi respuesta a Alexis fue acerca de cómo calcular ese límite. Para calcular el límite seguro tenés que utilizar de alguna forma los dos comportamientos de la función, que uno va a suceder cuando te acercás por una dirección (v_1,v_2) con v_1 \neq 0 y el otro cuando v_1=0.

Saludos,
Leandro
En respuesta a Leandro Bentancur

Re: Ej 4)b

de Federica Pereira Piñeyrua -
Hola una pregunta, estaba leyendo y me surgió la duda. Al calcular los limites direccionales teniendo un v=(v1,v2) general, siempre tenes que estudiarlo de forma que tengas las dos situaciones de la función?, por ejemplo en este caso agarraste que v1=0 para usar la función como "y" y el caso v1 ≠0 para usar la función como en el primer renglón. O sea para que tengas los dos casos de la función?. Después tenia una pregunta con respecto a los resultados, si estos dos casos, cuando v1=0 y v1≠0, te tienen que dar igual el limite o no es necesario. Desde ya gracias.
En respuesta a Federica Pereira Piñeyrua

Re: Ej 4)b

de Leandro Bentancur -
Hola Federica,
Sobre la primera duda, eso tenés que hacerlo cuando estás calculando las derivadas direccionales sobre un punto de forma que la fórmula que define la función varía según por que dirección te acerques.
Sobre la segunda, no tiene por qué dar igual, porque son derivadas direccionales para direcciones distintas.
Saludos,
Leandro