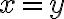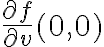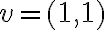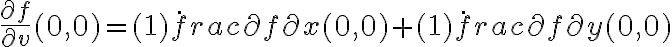Buenas,
Este ejercicio lo pense de la siguiente forma:
Como es diferenciable existe el gradiente. Por linealidad de derivadas la derivada direccional en v de (0,0) = derivada parcial de x en (0,0).
La derivada direccional en v de (0,0) la puedo calcular como <gradiente(0,0) , v>. Hasta aca me quedo, porque para calcular el gradiente necesito las derivadas parciales de x y de y pero la de x en (0,0) no la se ya que la derivada de x en (0,0) no puedo calcularla porque f(x,x) no tiene el segundo termino constante.
Como puedo terminar esto?
Gracias.