Foro Práctico 8

Hola Emanuel,

Al calcular las derivadas direccionales, supongamos en el primer caso que es un punto de la forma 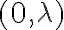$(0,\lambda)$, cuando evaluás 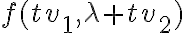$f(tv_1,\lambda + tv_2)$ va a depender de 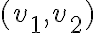$(v_1,v_2)$ si estás en un punto con 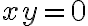$xy=0$ o no, es decir, cuál de las dos fórmulas de la función tenés que usar. Si 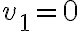$v_1 = 0$, entonces 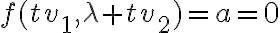$f(tv_1,\lambda + tv_2) = a =0$ y existe la derivada direccional (la función es cte en esa dirección). Esto se repite para los casos 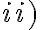$ii)$ y $iii)$.

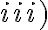Luego cuando estás calculando el límite para el caso 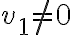$v_1 \neq 0$, que es el que desarrollaste, ese límite no no existe, te queda que tiende a una constante no nula multiplicada por algo que oscila. Esto se repite para el caso $ii)$.

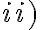Luego otro comentario es que dejás implícito que la función es continua y que existen todas las derivadas direccionales para los puntos con 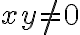$xy \neq 0$, asumo que lo sabés pero lo comento por las dudas porque en el caso de escribir una solución al ejercicio habría que incluirlo.

Saludos,

Leandro