Hola buenas, quería preguntaba por este ejercicio ya que no entiendo por que en la solución se llega a que solo se puede calcular el gradiente en el punto (0,1), por qué no podría hacerlo en el (0,2) por ejemplo.
desde ya gracias
Hola buenas, quería preguntaba por este ejercicio ya que no entiendo por que en la solución se llega a que solo se puede calcular el gradiente en el punto (0,1), por qué no podría hacerlo en el (0,2) por ejemplo.
desde ya gracias
 sólo la podemos calcular en los puntos de la forma
sólo la podemos calcular en los puntos de la forma 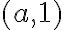 y la derivada parcial en
y la derivada parcial en  en los puntos de la forma
en los puntos de la forma 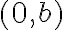 . En el punto
. En el punto 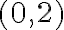 por ejemplo no sabemos la derivada en función de
por ejemplo no sabemos la derivada en función de  , porque dentro de un entorno pequeño del punto sólo sabemos el comportamiento de la función sobre el eje vertical y no sabemos nada en ninguna otra dirección.
, porque dentro de un entorno pequeño del punto sólo sabemos el comportamiento de la función sobre el eje vertical y no sabemos nada en ninguna otra dirección.Buenas,
Sobre la primera duda, como la derivada parcial en  se define como
se define como 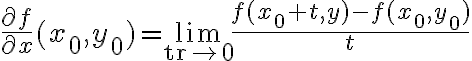 , entonces precisamos saber cómo se comporta la función en la recta
, entonces precisamos saber cómo se comporta la función en la recta 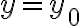 en un entorno del punto
en un entorno del punto 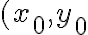 . Acá sobre los puntos de la recta
. Acá sobre los puntos de la recta 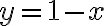 no sabemos esto (salvo en el
no sabemos esto (salvo en el 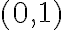 ).
).
Sobre la segunda duda, es así sí. Lo más correcto sería decir que es el único punto donde sabemos que existen, en realidad podría existir en otros puntos pero no tenemos la información.
Saludos,
Leandro