Buenas, tengo una duda sobre el siguiente ejercicio:
Estudié la continuidad de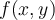 
y me dio que lo es sii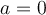 
Luego, al tratar de hallar las derivadas direccionales llego a lo siguiente:
Tengo que seguir desarrollando el 
y que llegue a 
?
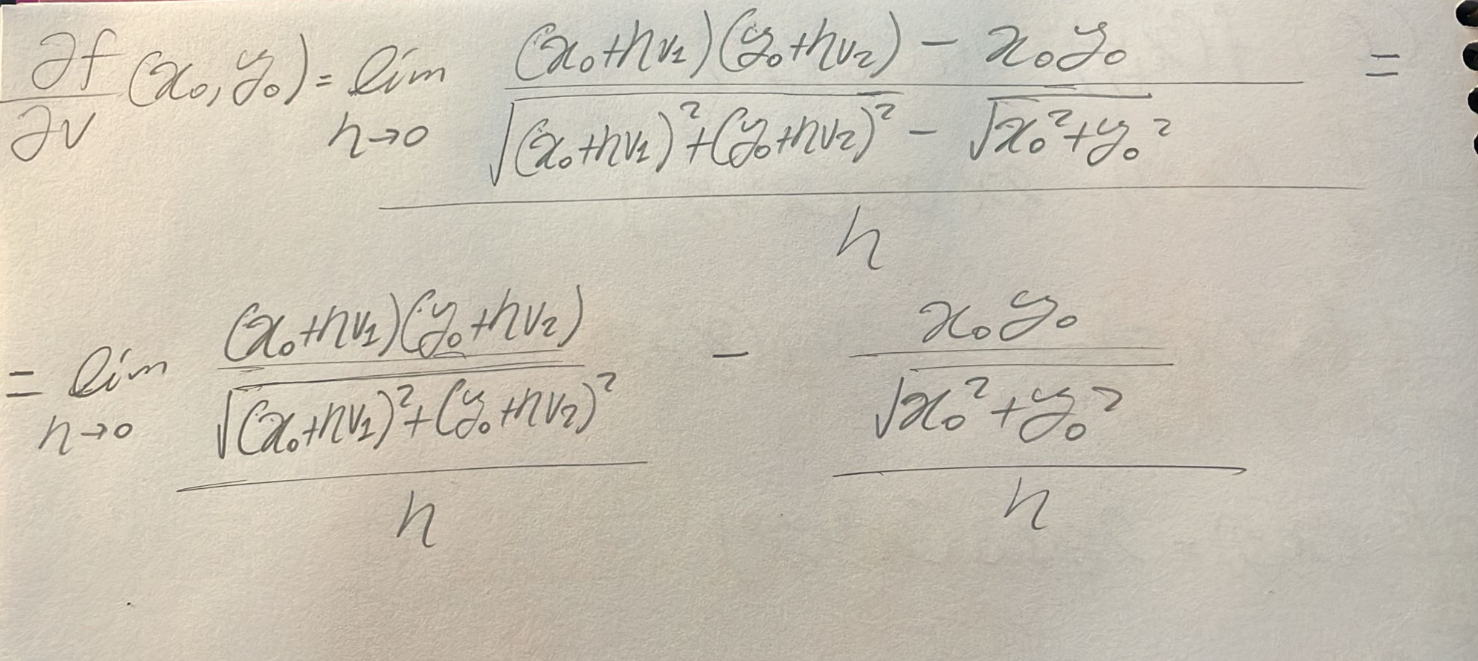
Hola Alexis,
Fuera del origen la función es diferenciable y las derivadas direccionales las podemos obtener como combinación lineal de las derivadas parciales. Así que lo que tenemos que calcular utilizando el límite es para el punto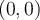 
, ahí te va a quedar más sencillo, y seguís hasta resolver el límite.
Saludos,
Leandro
Buenas! Estoy intentado con el mismo ejercicio y llegué a esto:
Como me doy cuenta que v debe ser (λ,0) o (0,µ)?
Como me doy cuenta que v debe ser (λ,0) o (0,µ)?
Hola Julieta,
Hay un detalle cuando sacás el
de la raíz, 
es 
. De ahí te va a surgir que el numerador tiene que anularse para que te quede igual el límite cuando tiende a por izquierda y por derecha.
Saludos,
Leandro
Hay un detalle cuando sacás el
de la raíz, es . De ahí te va a surgir que el numerador tiene que anularse para que te quede igual el límite cuando tiende a por izquierda y por derecha.Saludos,
Leandro
Buenas Leandro,
No me queda claro como seguir luego del comentario que le hiciste a julieta. El limite quedaria como el que hizo ella pero con h en el numerador y |h| en el denominador. Luego como sigo desde ahi?
Gracias
No me queda claro como seguir luego del comentario que le hiciste a julieta. El limite quedaria como el que hizo ella pero con h en el numerador y |h| en el denominador. Luego como sigo desde ahi?
Gracias
Buenas,
Exacto, y
es el signo de , es decir, vale 
si 
y vale 
si . Allí si querés podés separar el límite en 
y 
, y luego tener en cuenta de que el límite con 
existe si y sólo si los limites laterales existen y coinciden.
Saludos,
Leandro
Exacto, y
es el signo de , es decir, vale si y vale si . Allí si querés podés separar el límite en y , y luego tener en cuenta de que el límite con existe si y sólo si los limites laterales existen y coinciden.Saludos,
Leandro
Buenas,
a menos que alguien nos diga, que manera tenemos de verificar que una función es diferenciable? Tenemos que ir directo a la definición y probar que el resto tiende a cero mas rapido que el incremento?
a menos que alguien nos diga, que manera tenemos de verificar que una función es diferenciable? Tenemos que ir directo a la definición y probar que el resto tiende a cero mas rapido que el incremento?
Buenas,
Las formas más sencillas son viendo que se descompone en funciones más sencillas que son diferenciables (sumas, productos, composiciones) o utilizar el criterio de que las derivadas parciales son continuas en un entorno (y ahí de nuevo podés ver que las derivadas parciales son continuas descomponiéndolas en funciones más elementales que ya sepamos que son continuas). Cuando esos criterios no nos funcionan, esto es por ejemplo cuando la función está definida de forma partida y estamos en un punto que esté entre dos regiones, allí lo probamos con la definición, es decir, viendo que el resto tiende a cero más rápido que la norma del incremento como decís (para eso primero vemos las derivadas parciales para poder calcular el resto).
Saludos,
Leandro
Las formas más sencillas son viendo que se descompone en funciones más sencillas que son diferenciables (sumas, productos, composiciones) o utilizar el criterio de que las derivadas parciales son continuas en un entorno (y ahí de nuevo podés ver que las derivadas parciales son continuas descomponiéndolas en funciones más elementales que ya sepamos que son continuas). Cuando esos criterios no nos funcionan, esto es por ejemplo cuando la función está definida de forma partida y estamos en un punto que esté entre dos regiones, allí lo probamos con la definición, es decir, viendo que el resto tiende a cero más rápido que la norma del incremento como decís (para eso primero vemos las derivadas parciales para poder calcular el resto).
Saludos,
Leandro