Buenas!
Estoy intentando hacer el ejercicio 1, vi que lo que piden es lo que se hizo en la clase 16 de Openfing 2018, sin embargo me sigue costando un poco el entender los argumentos.
Lo que más me cuesta es lo que está con un " ( * ) " al costado, la parte en la que se afirma "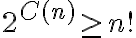
".
Si pudieran ver si lo que hice está más o menos bien y explicarme esa parte les agradecería!
Saludos!
Hola Esteban,
La solución en aspectos generales está bien.
Me confunden un poco las cuentas del final. Yo trabajaría sin los Omega desde el principio, acotando inferiormente C(n) y luego al final concluiría lo de Omega.
Respecto a lo que señalas en (*), lo que estás diciendo ahí es que un algoritmo S que ejecuta un máximo de C(n) comparaciones, es capaz de distinguir a lo sumo entre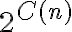
permutaciones. Esto es porque cada posible resultado de la secuencia de comparaciones, es capaz de distinguir una única permutación. Entonces, para poder distinguir entre todas las posibles permutaciones, la cantidad 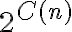debe ser mayor a 
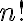(la cantidad de permutaciones posibles).
Espero que se haya entendido, cualquier cosa volvé a consultar.
Saludos,
Guillermo
La solución en aspectos generales está bien.
Me confunden un poco las cuentas del final. Yo trabajaría sin los Omega desde el principio, acotando inferiormente C(n) y luego al final concluiría lo de Omega.
Respecto a lo que señalas en (*), lo que estás diciendo ahí es que un algoritmo S que ejecuta un máximo de C(n) comparaciones, es capaz de distinguir a lo sumo entre
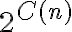permutaciones. Esto es porque cada posible resultado de la secuencia de comparaciones, es capaz de distinguir una única permutación. Entonces, para poder distinguir entre todas las posibles permutaciones, la cantidad 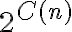debe ser mayor a 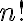(la cantidad de permutaciones posibles).Espero que se haya entendido, cualquier cosa volvé a consultar.
Saludos,
Guillermo