Buenas de nuevo!
Quería saber si el argumento que se me ocurrió para poder acotar el tiempo inferiormente es válido, pues al principio sólo se me ocurrían justificaciones utilizando "Divide y Vencerás" o "Búsqueda Binaria" y creo que no era a lo que se apuntaba.
Mi argumento fue el siguiente:
i) Dado un 
, al elegir la posición de 
en la que estaría la primer ocurrencia de 
y decidir si está o no (si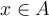 
o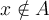 
), ya quedaría determinado un orden de según un dado.
Entonces, por cada arreglo de tamaño 
, tenemos posibles lugares para la primer ocurrencia de , y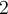 
posibilidades ( está o no).
Por lo tanto, hay 
posibles órdenes de un arreglo , según un dado.
ii) Como por cada comparacion que hace B, tiene 2 posibilidades, B a lo sumo distingue entre 
ordenes.
Como tiene que identificar uno de los posibles órdenes según 
.
Hola Esteban,
Tu razonamiento tiene aciertos, pero creo que hay algunas cosas que se están mezclando con la demostración de la cota inferior para los algoritmos de ordenamiento.
En principio, no entiendo qué querés decir con "..., ya quedaría determinado un orden de según un dado.".
El algoritmo de búsqueda binaria tiene que ser capaz de distinguir a partir de
comparaciones, posibles posiciones del arreglo. Con esa información, y con la hipótesis del tamaño del alfabeto (tener en cuenta que con tamaño de alfabeto menor o igual a 2, no se cumple), deberías poder hacer la demostración, sin pasar por el concepto de "orden".
Cualquier duda volvé a consultar.
Saludos,
Guillermo
Tu razonamiento tiene aciertos, pero creo que hay algunas cosas que se están mezclando con la demostración de la cota inferior para los algoritmos de ordenamiento.
En principio, no entiendo qué querés decir con "..., ya quedaría determinado un orden de
según un dado.".El algoritmo de búsqueda binaria tiene que ser capaz de distinguir a partir de
comparaciones, posibles posiciones del arreglo. Con esa información, y con la hipótesis del tamaño del alfabeto (tener en cuenta que con tamaño de alfabeto menor o igual a 2, no se cumple), deberías poder hacer la demostración, sin pasar por el concepto de "orden".Cualquier duda volvé a consultar.
Saludos,
Guillermo