hola, en el video sobre Complejidad de Algoritmos de Ordenamiento en el minuto 41 se discute la cantidad de cadenas distinas sobre el alfabeto A(que supongo que tenga cardinal 26(a,b,c,...,z)) y llegamos a que hay 
cadenas distintas, no logro enteder como se hizo esta cuenta, lo unico que pude llegar fue 
, contando la ocurrencia de cada letra del alfabeto, quisiera saber como se llega a esta cantidad.
Saludos, Pedro.
Hola Pedro,
El valor de es la cantidad de cadenas distintas que se pueden armar con un alfabeto finito de tamaño 
.
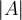Se puede llegar al cálculo pensando que para cada posición
hay 
posibles valores que puede asumir el símbolo. De esa manera la cantidad secuencias distintas está dada por 
veces.
Espero que haya quedado claro, cualquier cosa volvé a consultar.
Saludos,
Guillermo
El valor de
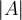es la cantidad de cadenas distintas que se pueden armar con un alfabeto finito de tamaño . Se puede llegar al cálculo pensando que para cada posición
hay posibles valores que puede asumir el símbolo. De esa manera la cantidad secuencias distintas está dada por veces.Espero que haya quedado claro, cualquier cosa volvé a consultar.
Saludos,
Guillermo
quedo claro, muchas gracias!