Foro Práctico 8

Buenas tardes, no entiendo el siguiente resultado: 

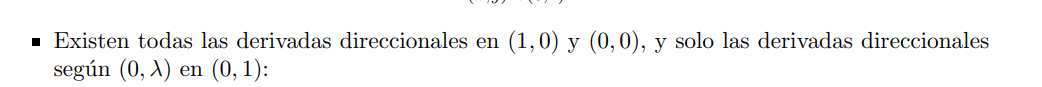
No comprendo cómo existen las derivadas direccionales en 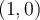$(1,0)$ , estoy tratando de darme cuenta analíticamente con la definición de la siguiente manera:

$\frac{ \partial f}{ \partial v} (1,0) = \lim_{h \to 0} \frac{ f(x_0 + hv_1 , hv_2) - f(1,0)}{h}$

Entonces suplanto los valores en $f$ y me queda el siguiente límite:

$\lim_{h \to 0} \frac{[(x_0 + hv_1)^2 + h^2 v_2 ^2 ]\sin( \frac{1}{x_0 + hv_1} ) + e^{(x_0 + hv_1)hv_2}- \ (\sin(1)+1)}{h}$

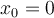Traté de desarrollar el cuadrado, que me da $(x_0 ^2 + 2x_0 hv_1 + h^2 v_1 ^2)...$ Luego no sé cómo más seguirlo o si está bien, porque el $x_0 ^2$ no veo que se me vaya, entonces me complica todo , si supongo que $x_0 = 0$ me queda una 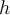$h$ arriba que multiplica al 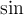$\sin$ y me quedaría cero por acotado, supongo, entonces en el numerador me queda $e^0 - ( \sin(1) + 1) = - \sin(1)$ , no veo otra forma de darme cuenta