Tengo dudas sobre el estudio si la función es diferenciable en el punto (x,1), según tengo entendido, si existen las derivadas parciales en un entorno de (x,1), y ambas son continuas en (x,1) entonces f es diferenciable y por ende existen todas las derivadas direccionales en (x,1).
Sin embargo, al ver la respuesta no existen todas las derivadas direccionales en el punto (x,1), ya que me condiciona el para todo (x,1), es decir, existen todas solamente para los (x,y) tal que y es distinto de 1, unión (0,1), por lo tanto no se estaria cumpliendo para todo (x,1).
Hice esto:
Hola Juan,
Sobre la duda, si la función es diferenciable en un punto, entonces existen todas las derivadas direccionales en ese punto. Por lo tanto, por el contrarrecíproco, si no existe alguna derivada direccional en un punto, entonces la función no es diferenciable allí.
Sobre la imagen,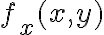
la calculaste para los puntos con 
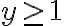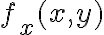y la calculaste para los puntos con 
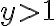, porque utilizaste la fórmula 
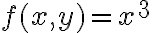y esos son los puntos donde corresponde hacerlo con esa fórmula. Cuando escribís los límites no tengo claro qué es lo que estás haciendo. Si estás estudiando la continuidad entonces deberías calcular la derivada parcial en los puntos que no la calculaste y luego en el punto 
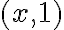para verificar que el límite de la derivada parcial vale lo mismo que la derivada parcial en el punto. Lo de calcular el límite por derecha e izquierda lo podemos hacer cuando estamos en una sola variable, porque allí tenemos sólo dos formas de aproximarnos a un punto, en el plano no podemos hacer lo mismo.
Saludos,
Leandro
Sobre la duda, si la función es diferenciable en un punto, entonces existen todas las derivadas direccionales en ese punto. Por lo tanto, por el contrarrecíproco, si no existe alguna derivada direccional en un punto, entonces la función no es diferenciable allí.
Sobre la imagen,
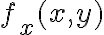la calculaste para los puntos con 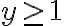y 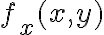la calculaste para los puntos con 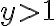, porque utilizaste la fórmula 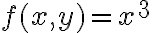y esos son los puntos donde corresponde hacerlo con esa fórmula. Cuando escribís los límites no tengo claro qué es lo que estás haciendo. Si estás estudiando la continuidad entonces deberías calcular la derivada parcial en los puntos que no la calculaste y luego en el punto 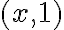para verificar que el límite de la derivada parcial vale lo mismo que la derivada parcial en el punto. Lo de calcular el límite por derecha e izquierda lo podemos hacer cuando estamos en una sola variable, porque allí tenemos sólo dos formas de aproximarnos a un punto, en el plano no podemos hacer lo mismo.Saludos,
Leandro